본 포스팅은 충남대 고영준 교수님의 강의자료를 바탕으로 작성한 글입니다.
2024.11.25 - [AI/영상처리] - Feature Matching
그럼 앞의 글에서 우린 feature 매칭을 했고, 이미지의 변환을 봤다.
이제 이미지를 어떻게 변환시켜 연결할지를 생각해야 한다.
I1를 I2에 이어붙이기 위해서, 사진 두 개만 가지고 내가 scaling을 얼마나 해야 하는지, translation을 얼마나 해야 하는지를 알아낼 수는 없다.
근데 잘 생각해보자. 우린 이미 feature matching이 끝난 상태이다.
즉, x'=Mx에서 x'와 x는 이미 아는 상태란 말이다.
그럼 이를 이용해 M을 구하면, x가 어떤 변형을 통해 x'가 되는지 알 수 있을 것이다.
뭐야 그럼 M = x'(x)^(-1)이네! 라고 쉽게 생각할 수 있겠지만, 이것이 아니다.
잘 따라와보면 이유를 알 수 있다.
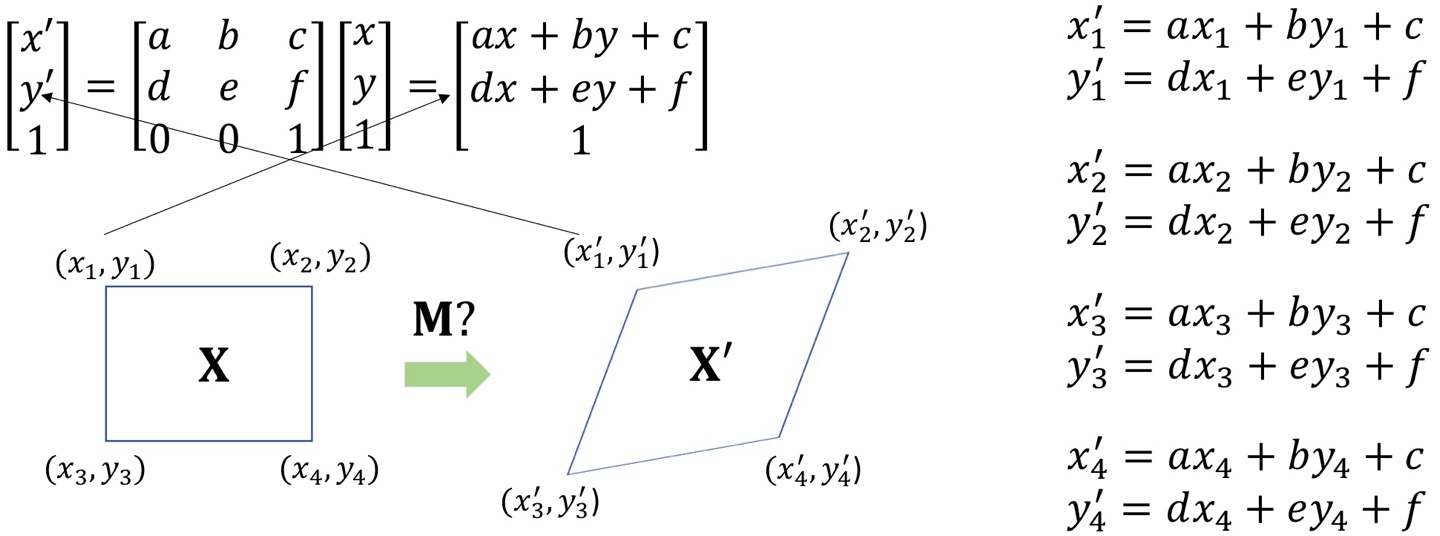
지금 이렇게 x와 x'들이 매칭된 상태이고, 이걸 x'=Mx의 형태로 나타내려면

이렇게 바꾸면 된다.
그냥 식 6개를 쓰면 theta가 더 빨리 구해지지 않을까?
라는 생각을 할 수도 있지만,
여기서 구하려는 건 정확한 theta가 아니라 최대한 loss를 줄이는 theta이다.
또한, 여기서 알 수 있듯 A가 m*6 형태이기에 역행렬을 만들 수 없다.

loss는 이렇게 구할 수 있고, 항상 하던 대로 이 loss를 최소화하기 위해 미분을 하겠다.
그럼 아래와 같은 식이 나오고, theta는 아래처럼 구할 수 있다.

따라서 feature matching 결과로 A와 b를 만든 후 식에 대입하면 theta를 구할 수 있다.
Finding Homography

H라는 행렬을 통해 tilda를 tilda_prime으로 바꿀 수 있다.
x_tilda_prime은 저렇게 행렬에서의 원소의 곱으로 나타낼 수 있고, y나 z도 마찬가지이다.
근데 여기서, x' = x_tilda'/z_tilda' 로 나타낼 수 있고, y도 마찬가지인데,
이를 적용한다면 x'과 y'을 아래와 같이 나타낼 수 있다.

만약 행렬 H에 일정한 상수가 모두 곱해진다고 해도, 어차피 x'와 y'에는 분자 분모에 같은 수가 곱해지는 것이기에 여전히 같다.
여기서 H에 대한 미지수를 줄일 수 있는 방법!
지금은 h11, h12... 이렇게 총 9개인데, 이 모든 걸 h33으로 나누면 h11/h33, h12/h33, ..., 1 이렇게 마지막 원소는 1이 된다!
그럼 그냥 h11 이런 애들을 구한다기 보다, h11/h33 -> a, h12/h33 -> b 이렇게 바꿔서 총 미지수를 8개로 만들어줄 수 있다.
그리고 x'에 대한 위 식에서도.. 분모 분자를 z_tilda로 나눠주면서 미지수를 줄일 수 있다.
그럼 결과적으로 이런 식이 나온다.
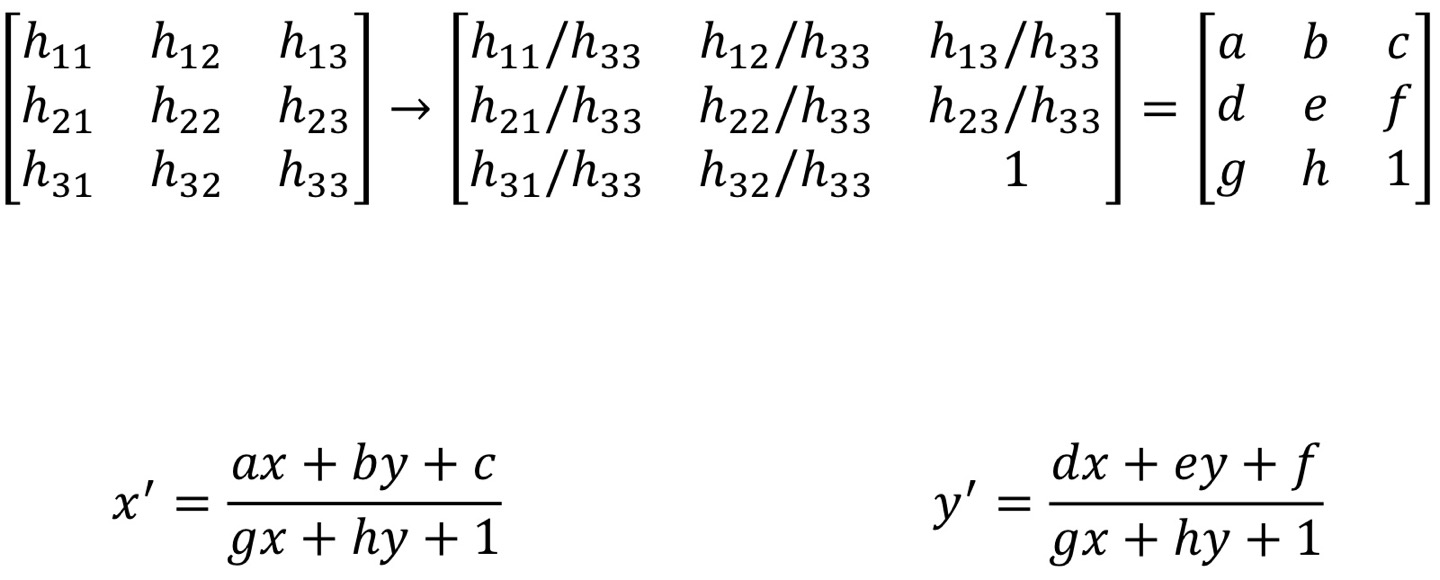
그럼 여기서 각 분모를 양변에 곱해주면 gxx' + hyx' + x' = ax + by + c가 되고,
x'만 남기고 이항시키면 x' = ax + by + c - gxx' - hyx' 가 된다.
y'도 마찬가지로 dx + ey + f - gxy' - hyy'가 된다.
그럼 이것들을 이제 행렬의 형태로 나타내보겠다! 그래야 a, b, c.. 이 미지수들을 구할 수 있기 때문이다.

이렇게 나타내면 딱 된다.
여기서도 아까의 그 의문이 드는 것이다.
어차피 미지수 8개인데,, 그냥 행도 8개 해서 미지수 구하면 안되나? 하는 것!
그치만 그게 안 되는 이유는, 이걸 아예 만족하는 미지수는 없다는 것이고, 그저 Loss를 최소화할 미지수를 구하고 싶은 것!
따라서 위에서 본 식처럼, theta = (a'a)^(-1)*A.T*b가 될 것~
Image Alignment (이미지 조정)
주어진 이미지 A와 B
1. A와 B의 keypoint같아보이는 점을 찾고 이를 묘사한다.
2. A와 B의 keypoint를 매칭한다.
3. A와 B 사이 매칭시의 최소제곱을 사용해 가장 작아지는 H를 추정한다.
여기서 주의해야할 점은, outlier 들!!!
최소'제곱'을 이용하기에, 이상치에 많이 민감하다. 즉, 이상치의 모델 기여도가 높다는 뜻이다.
따라서 이상치가 있더라도 민감하게 반응하지 않을 '견고함'이 필요하다.
RANSAC(RANdom SAmple Consensus)
랜덤으로 k이상 개수의 점들을 골라서 직선을 만든다.
1. 모델을 적합시키는 데 필요한 개수의 점을 샘플링한다.
2. 샘플들로 모델의 파라미터를 생각한다.
3. 미리 설정된 threshold 내에서 인라이어의 비율로 점수를 매긴다.
4. 위 1-3번을 반복하면서 가장 좋은 모델을 찾는다.

즉, 여기선 2개의 점 (노란색)을 sampling한 것이고,
그 둘로 만든 모델이 검정 선이고,
threshold를 적용시킨 범위가 파란색이고,
파란색 안에 들어온 데이터들이 inlier이다.
전체 중 inlier가 몇 개인지 그 비율을 따져서 점수를 매기면 된다.
inlier 개수를 count라 하고,
가장 count가 높을 때를 찾으면 된다! (보통 inlier 비율이 0.8 정도 되면 그거 쓰면 됨)
그리고, 이걸 실제 이미지에 대입해보면!

이렇게 되는데, 하나의 쌍을 기준으로 살펴보면, 지금은 초록 쌍을 선택한 것이다.
나머지 애들과 매칭된 방향을 따져보면, 얘는 방향이 비슷한 애가 하나밖에 없다. 즉 inlier가 2개인 것.
근데 만약 저 맨밑의 쌍을 선택한다면, inlier가 5개가 될 것이다.
이렇게 모든 쌍에 대해 진행하고, inlier가 가장 많은 모델을 고른다.
그럼 그 모델에서의 이상치인 2개 쌍을 제외해버리면 된다.
<다시 보는 RANSAC 단계>
1. 세 개의 랜덤 쌍 선택
2. 최소제곱 이용해 M 계산 (H를 말함)
3. inlier 개수 계산 (threshold 통과된)
4. inlier가 늘어날 때마다 H 재계산
'AI > 컴퓨터비전' 카테고리의 다른 글
| Vision Transformer (0) | 2024.12.16 |
|---|---|
| Image Warping (new!) (0) | 2024.12.16 |
| SIFT (0) | 2024.12.16 |
| Image Classification (0) | 2024.12.15 |
| Image segmentation (3) | 2024.12.09 |
