Image classification
이미지 분류가 어려운 이유는,
일단 컴퓨터에게는 이미지가 각 픽셀이 숫자로 보이고,
이미지 자체도 어느 방향에서 찍느냐에 따라 다른 이미지처럼 보이기 때문이다.
아니면 뭐 픽셀값이 배경과 유사해서 객체가 눈에 띄지 않는다거나, 배경에 가려질 수도 있다.
아니면 객체가 서있든 누워있든 자세가 변형되고, 특이한 모양의 객체가 있고, 같은 객체여도 품종이 다르고,
배경에 의해 다르게 인식되고(창틀의 그림자에 의해 개가 호랑이로 인식).. 등등의 문제가 있다.
우리는 그래서 이미지 분류를 위해 박스를 만든다.
이미지에 박스를 쳐서 그 박스가 배경에 해당하는지, 사람에 해당하는지.. 등등을 따진다.
그리고 captioning을 하는데, 이건 그 이미지를 언어로 표현한다고 생각하면 된다.
예를 들어, '어떤 남자가 말을 타는 사진' 이런 식으로 말이다.
'Man riding'까지의 문장이 있다면, 이 뒤에 horse를 붙이는 형식으로 진행할 수 있다.
뭐 숫자를 센다거나.. 그런 것과는 달리,
이미지에서 클래스를 인식하는 알고리즘을 하드코딩하는 방법은 딱히 없다.
데이터 기반 접근
1. 이미지들과 라벨을 모은다.
2. 기계학습 알고리즘으로 분류기를 학습시킨다.
3. 새로운 이미지로 분류기를 평가한다.
보통 Input이 들어오면 수작업으로 특성을 추출하고, 머신러닝 돌리고, Output을 내서 평가한다.
그럼 그 분류기의 평가 매트리은 어떻게 되느냐 하면,
Accuracy, 즉 #correct/#sample로 계산하면 된다.
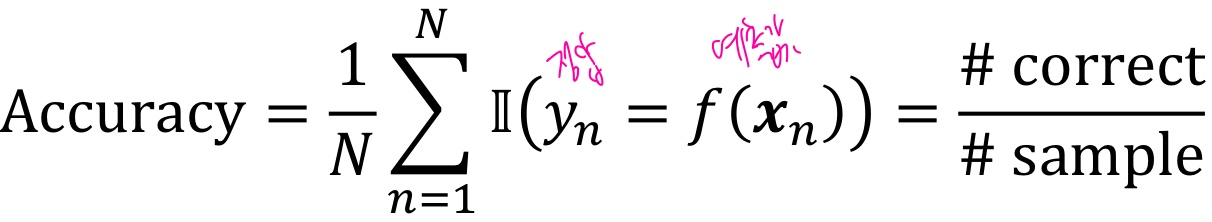
이진지시함수 Ic는 조건 c가 참이면 1, 아니면 0을 반환한다.
그리고 이와 비슷한 매트릭으로, Error rate가 있다.
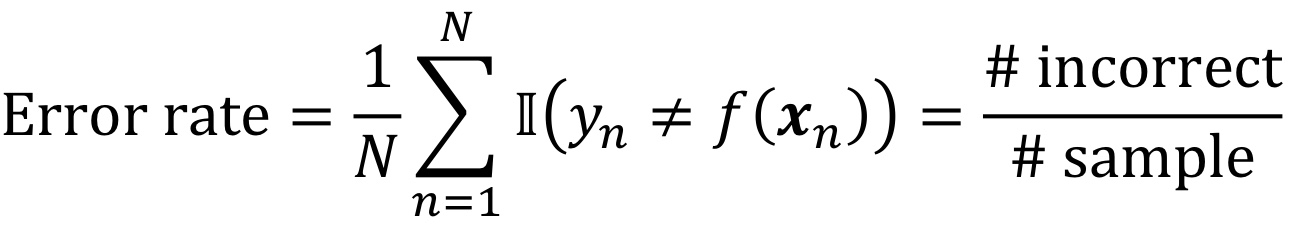
Linear classifier
Neural Network는 Linear classifier를 여럿 쌓은 것이다.
파라미터식 접근은,
Image를 flatten 시키고, f(x, W)에서 x는 Image, W는 parameter이다.
만약 2*2 image이고, 3classes라면,
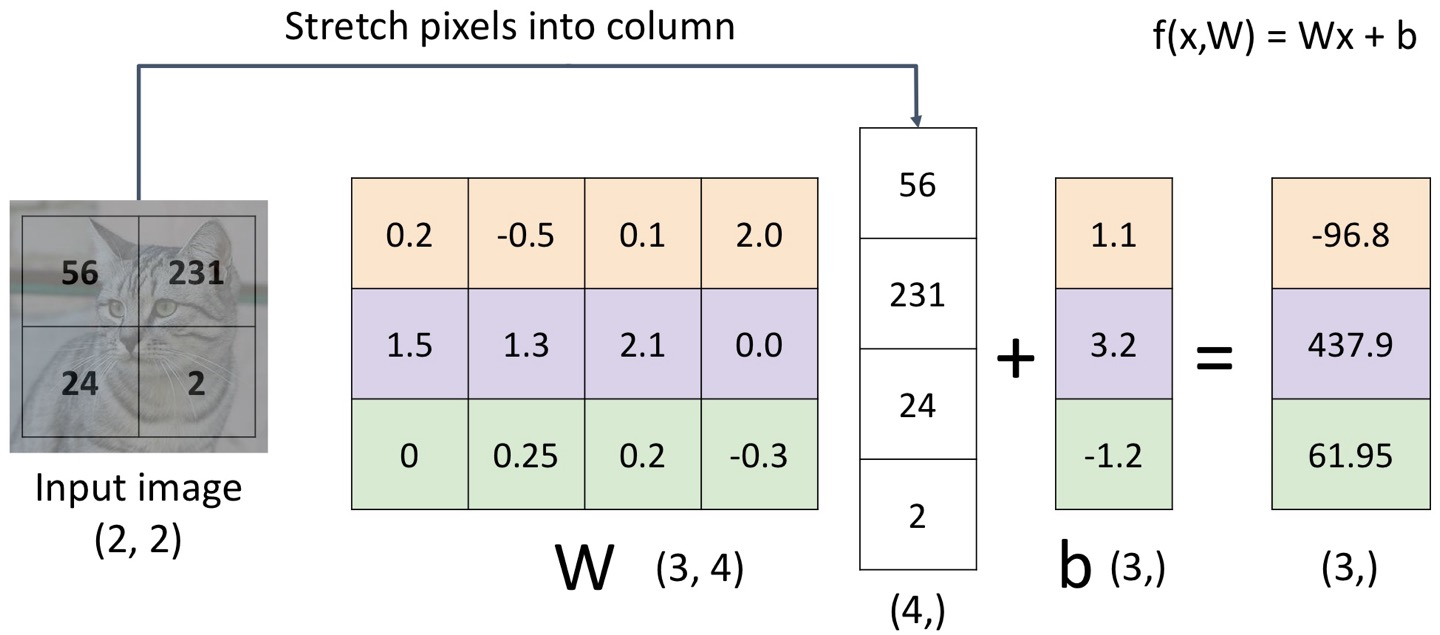
일단 2*2 -> (4, )로 flatten 시키고,
가중치는 W, (3, 4)이며,
이 가중치 (3, 4)와 위의 (4, )를 곱해서 상수항인 b(3, )를 더하면 결과적으로 (3, ) 형태가 나온다.
여기서 이 3은 #class 이다.
근데 이러면 문제점이, 선형이 아니라는 것이다.
따라서 이걸 Wx+b가 아니라 그냥 Wx 형태로 바꾸기 위해,
W를 (3, 5)로 만들고, (4, )를 밑에 1을 합쳐서 (5, )로 바꾼다.
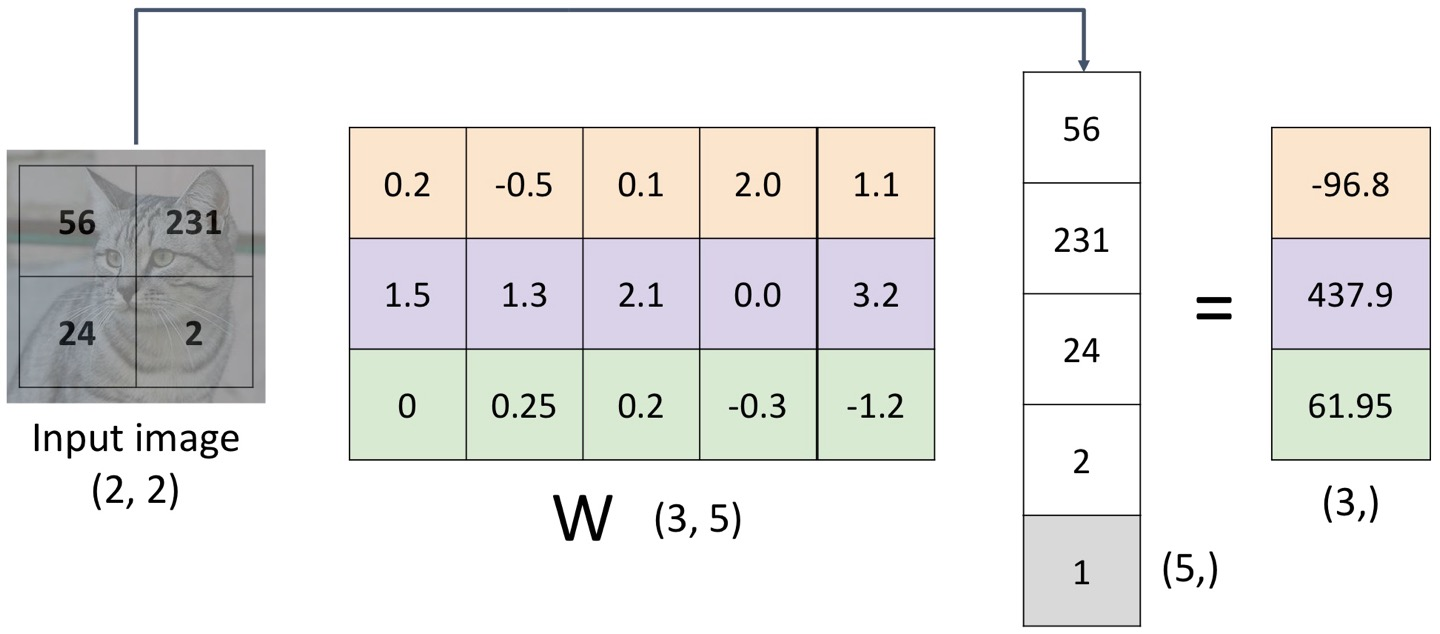
이렇게 말이다.
왜 굳이 이렇게 하냐, 하면은
이미지에 선형 변환 ex) 전체적으로 0.5 곱하기 or 0.5 더하기 등
을 했을 때, Output도 똑같은 변환만 거치면 되기 때문이다.
W만 주어지면 우린 image x에 대한 class score를 계산할 수 있다.
그렇다면 W를 어떻게 구하는가?..
1. 손실 함수를 이용해 W에 대한 좋은 가치가 무엇인지 측정하여 최적화 문제를 정의한다.
2. 손실 함수를 최소화하는 W를 찾는다.
손실함수
이건 우리의 분류기가 얼마나 좋은지를 말하는 것.
Loss가 낮으면 좋은 분류기인 것임~
xi가 image, yi가 label일 때, Loss는 L(f(xi, W), yi)로 주어진다.
Multiclass SVM classifier

여기서 Yi는 그 클래스의 label이고, j는 yi가 아닌 다른 라벨을 말한다.
max(0, 5.1-3.2+1)은 car와 cat을 비교한 것, 그 밑은 frog와 cat을 비교한 것인데,
따라서 만약 cat이 가장 높게, 두 번째보다 높은 것에 +1된 값보다 높다면,
Loss function은 항상 0이 나올 것이다.
예를 들어 옆의 car를 예측하는 모델의 loss에서, 두 번째로 높은 값인 frog 보다 1 높은 3보다 car의 값이 높으므로..
여기선 loss가 항상 0이 된다.
frog를 구분하는 것은.. 그냥 진짜 이상하게 됐으니까 loss가 엄청 높게 나온다.
그럼 최종적으로 cat을 구할 때의 loss, car를 구할 때의 loss, frog를 구할 때의 loss 이 세 가지를 평균내면 최종 Loss이다.
Softmax Classifier
이건 약간 다르게, 위처럼 결과가 나왔다면,
일단 cat을 분류하는 문제를 봤을 때 각 값이 3.2, 5.1, -1.7인데 얘네를 다 지수함수에 적용시킨다.
그럼 24.5, 164.0, 0.18이 나오고, 이를 정규화(자기자신/합)한다 (Softmax) -> 0.13, 0.87, 0.00 (확률이 됨!)
이렇게 출력된 결과를 실제 확률인 1, 0, 0과 쿨백라이블러 발산을 이용해 비교한다.
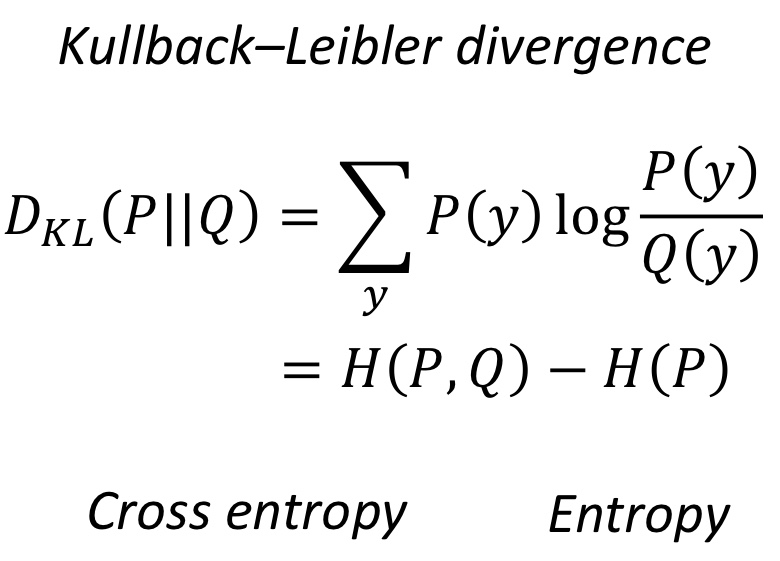
여기서 Cross entropy는 아래 사진과 같이 구할 수 있다.
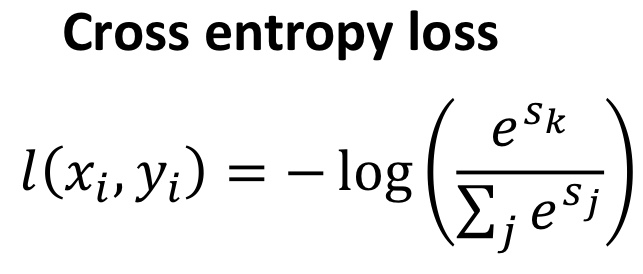
즉, Cross-entropy loss와 SVM loss를 비교하자면,
SVM loss은 잘 분류했든 못 분류했든 정답만 맞으면 모두 0이 되는데,
CE loss는 다른 게 커지면 내가 작아지는.. 그런 게 있기에 좋음
'AI > 컴퓨터비전' 카테고리의 다른 글
| Image Alignment (1) | 2024.12.16 |
|---|---|
| SIFT (0) | 2024.12.16 |
| Image segmentation (3) | 2024.12.09 |
| CNN, Architectures (0) | 2024.12.09 |
| Feature Matching (1) | 2024.11.25 |
Image classification
이미지 분류가 어려운 이유는,
일단 컴퓨터에게는 이미지가 각 픽셀이 숫자로 보이고,
이미지 자체도 어느 방향에서 찍느냐에 따라 다른 이미지처럼 보이기 때문이다.
아니면 뭐 픽셀값이 배경과 유사해서 객체가 눈에 띄지 않는다거나, 배경에 가려질 수도 있다.
아니면 객체가 서있든 누워있든 자세가 변형되고, 특이한 모양의 객체가 있고, 같은 객체여도 품종이 다르고,
배경에 의해 다르게 인식되고(창틀의 그림자에 의해 개가 호랑이로 인식).. 등등의 문제가 있다.
우리는 그래서 이미지 분류를 위해 박스를 만든다.
이미지에 박스를 쳐서 그 박스가 배경에 해당하는지, 사람에 해당하는지.. 등등을 따진다.
그리고 captioning을 하는데, 이건 그 이미지를 언어로 표현한다고 생각하면 된다.
예를 들어, '어떤 남자가 말을 타는 사진' 이런 식으로 말이다.
'Man riding'까지의 문장이 있다면, 이 뒤에 horse를 붙이는 형식으로 진행할 수 있다.
뭐 숫자를 센다거나.. 그런 것과는 달리,
이미지에서 클래스를 인식하는 알고리즘을 하드코딩하는 방법은 딱히 없다.
데이터 기반 접근
1. 이미지들과 라벨을 모은다.
2. 기계학습 알고리즘으로 분류기를 학습시킨다.
3. 새로운 이미지로 분류기를 평가한다.
보통 Input이 들어오면 수작업으로 특성을 추출하고, 머신러닝 돌리고, Output을 내서 평가한다.
그럼 그 분류기의 평가 매트리은 어떻게 되느냐 하면,
Accuracy, 즉 #correct/#sample로 계산하면 된다.
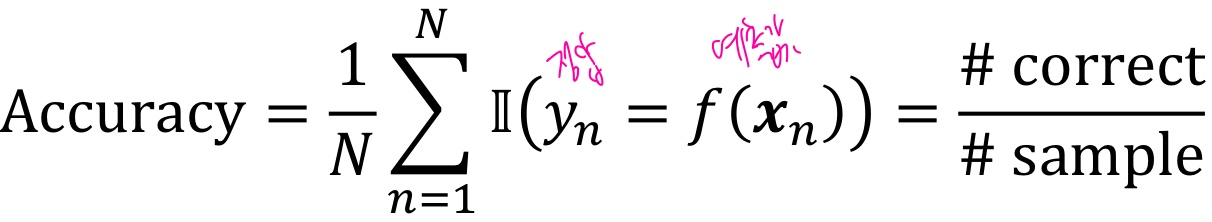
이진지시함수 Ic는 조건 c가 참이면 1, 아니면 0을 반환한다.
그리고 이와 비슷한 매트릭으로, Error rate가 있다.
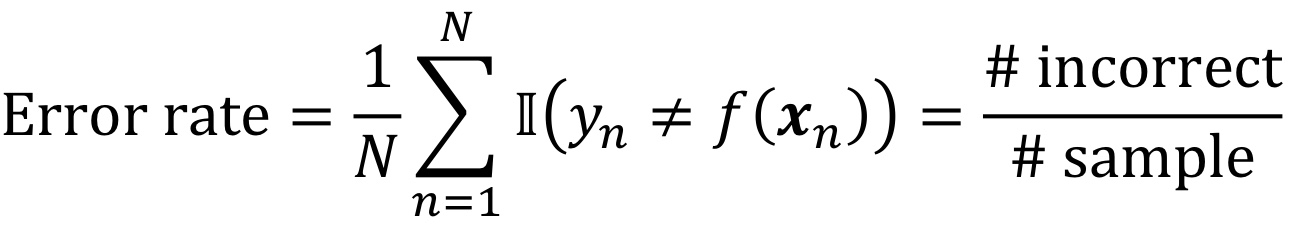
Linear classifier
Neural Network는 Linear classifier를 여럿 쌓은 것이다.
파라미터식 접근은,
Image를 flatten 시키고, f(x, W)에서 x는 Image, W는 parameter이다.
만약 2*2 image이고, 3classes라면,

일단 2*2 -> (4, )로 flatten 시키고,
가중치는 W, (3, 4)이며,
이 가중치 (3, 4)와 위의 (4, )를 곱해서 상수항인 b(3, )를 더하면 결과적으로 (3, ) 형태가 나온다.
여기서 이 3은 #class 이다.
근데 이러면 문제점이, 선형이 아니라는 것이다.
따라서 이걸 Wx+b가 아니라 그냥 Wx 형태로 바꾸기 위해,
W를 (3, 5)로 만들고, (4, )를 밑에 1을 합쳐서 (5, )로 바꾼다.

이렇게 말이다.
왜 굳이 이렇게 하냐, 하면은
이미지에 선형 변환 ex) 전체적으로 0.5 곱하기 or 0.5 더하기 등
을 했을 때, Output도 똑같은 변환만 거치면 되기 때문이다.
W만 주어지면 우린 image x에 대한 class score를 계산할 수 있다.
그렇다면 W를 어떻게 구하는가?..
1. 손실 함수를 이용해 W에 대한 좋은 가치가 무엇인지 측정하여 최적화 문제를 정의한다.
2. 손실 함수를 최소화하는 W를 찾는다.
손실함수
이건 우리의 분류기가 얼마나 좋은지를 말하는 것.
Loss가 낮으면 좋은 분류기인 것임~
xi가 image, yi가 label일 때, Loss는 L(f(xi, W), yi)로 주어진다.
Multiclass SVM classifier

여기서 Yi는 그 클래스의 label이고, j는 yi가 아닌 다른 라벨을 말한다.
max(0, 5.1-3.2+1)은 car와 cat을 비교한 것, 그 밑은 frog와 cat을 비교한 것인데,
따라서 만약 cat이 가장 높게, 두 번째보다 높은 것에 +1된 값보다 높다면,
Loss function은 항상 0이 나올 것이다.
예를 들어 옆의 car를 예측하는 모델의 loss에서, 두 번째로 높은 값인 frog 보다 1 높은 3보다 car의 값이 높으므로..
여기선 loss가 항상 0이 된다.
frog를 구분하는 것은.. 그냥 진짜 이상하게 됐으니까 loss가 엄청 높게 나온다.
그럼 최종적으로 cat을 구할 때의 loss, car를 구할 때의 loss, frog를 구할 때의 loss 이 세 가지를 평균내면 최종 Loss이다.
Softmax Classifier
이건 약간 다르게, 위처럼 결과가 나왔다면,
일단 cat을 분류하는 문제를 봤을 때 각 값이 3.2, 5.1, -1.7인데 얘네를 다 지수함수에 적용시킨다.
그럼 24.5, 164.0, 0.18이 나오고, 이를 정규화(자기자신/합)한다 (Softmax) -> 0.13, 0.87, 0.00 (확률이 됨!)
이렇게 출력된 결과를 실제 확률인 1, 0, 0과 쿨백라이블러 발산을 이용해 비교한다.
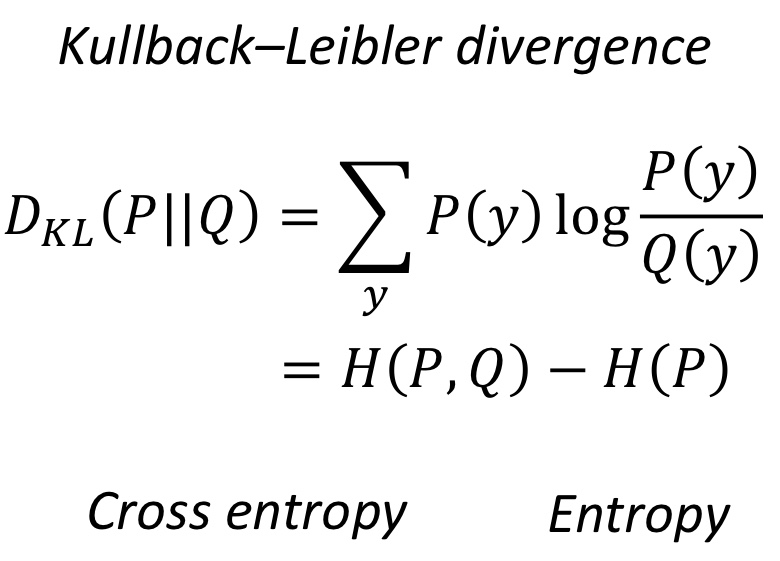
여기서 Cross entropy는 아래 사진과 같이 구할 수 있다.
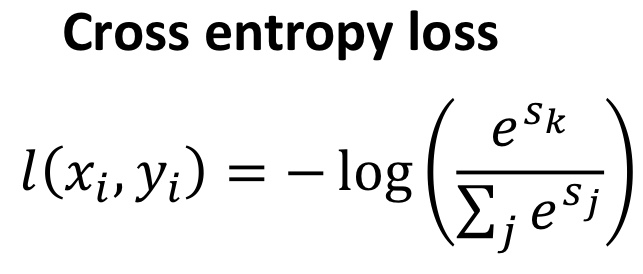
즉, Cross-entropy loss와 SVM loss를 비교하자면,
SVM loss은 잘 분류했든 못 분류했든 정답만 맞으면 모두 0이 되는데,
CE loss는 다른 게 커지면 내가 작아지는.. 그런 게 있기에 좋음
'AI > 컴퓨터비전' 카테고리의 다른 글
| Image Alignment (1) | 2024.12.16 |
|---|---|
| SIFT (0) | 2024.12.16 |
| Image segmentation (3) | 2024.12.09 |
| CNN, Architectures (0) | 2024.12.09 |
| Feature Matching (1) | 2024.11.25 |
