Scale-invariance corner detection
위치와 규모 모두에서 지역 최대값을 찾는 방법이다.
corner를 찾을 때, 만약 사진이 확대 또는 축소돼있다면..?
아래 그림과 같이, 코너를 넓은 공간에서 찾아야 하는지, 좁은 공간에서 찾아야 하는지가 달라진다.
LoG filter는 이렇게 생겼는데, original에 이를 적용시키면 아래 그림과 같이 된다.

Laplacian
유한한 뺄셈을 이용해서 1차 도함수 필터처럼 도출할 수 있다.

이런 식으로 말이다. 위는 1차 도함수, 밑은 2차 도함수를 필터로 나타내본 것이다.
Image에서는 이렇게 벡터 형태의 필터가 아니라, n*n 형태의 필터를 주로 사용하는데, 이는 아래와 같다.
Laplacian 필터이다.

f를 x^2로 편미분한 것은 y에는 영향을 끼치지 않고, f를 y^2로 편미분한 것은 x에는 영향을 끼치지 않는다.
그리고 f(x+1, y)는 laplacian 필터의 (2, 3)원소의 값을 의미한다.
중심을 f(x, y)라 했을 때 그보다 x좌표가 1 증가했기 때문!
영행렬에다, 각 좌표를 의미하는 곳에 곱해진 수만큼이 더해진다.
Laplacian of Gaussian (LoG) filter
위의 Laplacian filter를 사용한 것인데, 거기에 Gaussian filtering을 결합한 것!
일단 이미지에 Gaussian을 하여 smoothing을 먼저 하고, 이에 Laplacian을 결합한다.
그럼 아래처럼 결과적으로 zero-crossings at edges가 된다.

이렇게 Input에 원래 noise가 껴있는데, 그렇기에 만약 가우시안을 하지 않고 laplacian을 먼저 적용한다면?
웬만한 모든 곳이 변화가 있는 것으로 될 것이다. -> 가우시안 후 Laplacian! 순서 중요!
그럼 일일히 이미지에 가우시안과 Laplacian을 적용할 필요 없이, 가우시안 필터를 두 번 미분한 필터를 만들면 될 것이다.
이게 바로 LoG filter이다.
생김새는 위에 나와있는 그림과 같은데, sigma 값에 따라 폭이 변화한다.
signal이 filter와 동일한 특성 스케일을 가질 때의 응답이 가장 높다. 여기서 응답은 변화량을 의미한다.
이게 도대체 뭔 말이냐~면 이 LoG filter는 특징을 탐지하는 필터인데,
저 sigma에 따라 달라지는 LoG filter와, 특징의 signal 크기가 비슷하다면 그게 가장 잘 탐지된다는 뜻이다.

이런식으로, sigma=1인 LoG filter는 저 좁은 original signal에서 가장 잘 탐지한다.
그 '특징'이 무엇이고, 어떻게 구하냐 하면,
x축을 LoG filter의 sigma로, y축을 응답량으로 하는 그래프로 나타내보면 된다.
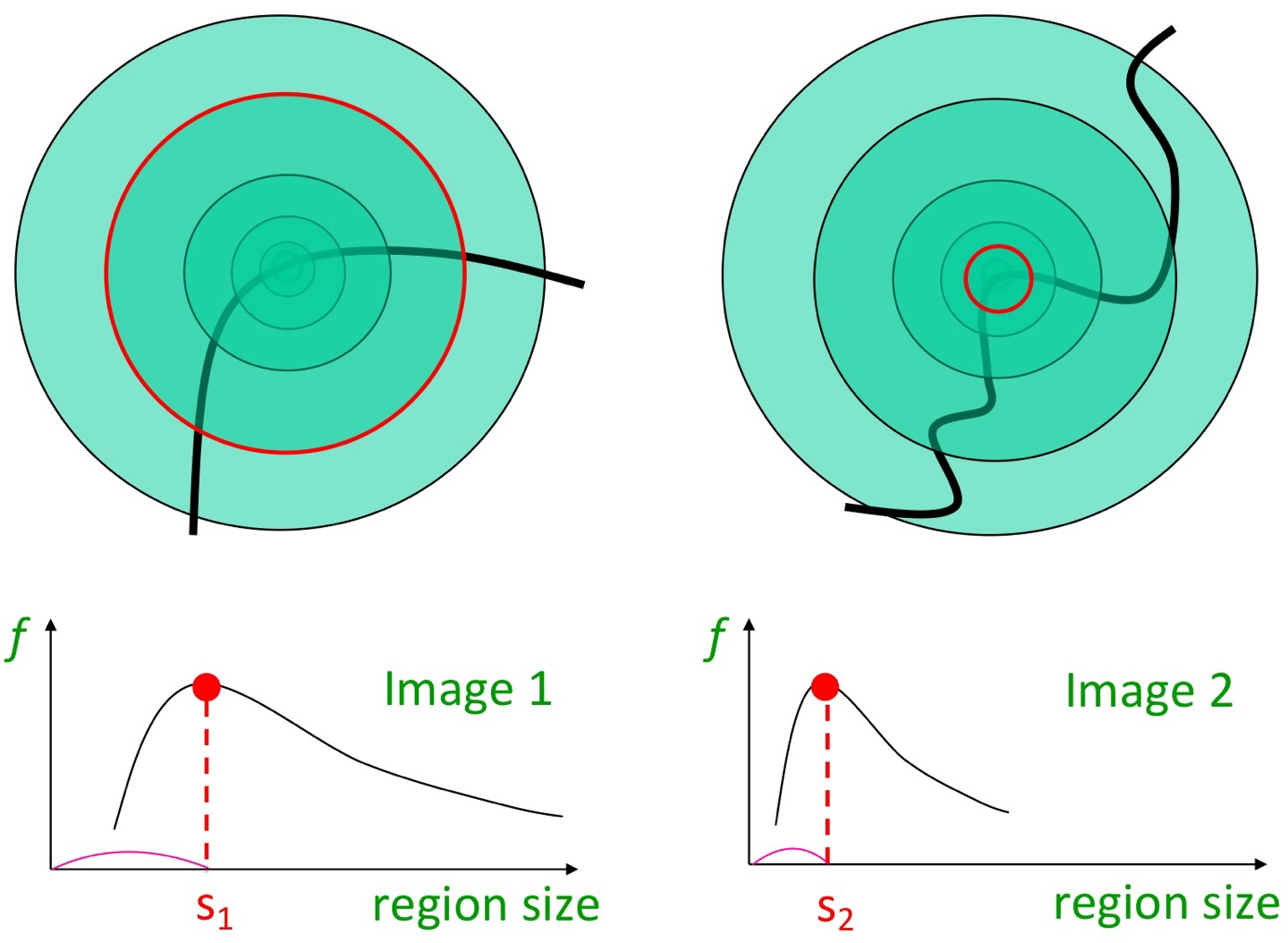
아래 예시를 봐보자.

여기서 나는 저 동그란 부분에 대해 특성을 찾아보고 싶다.
그럼 기준선을 정하자. 이 예시에서는 '수평선'을 기준으로 하겠다.
이 그래프는 무엇을 나타낸 거냐면, 만약 그래프의 x축 값이 1인 경우를 생각하면, 저 동그란 부분 안에 작은 필터를 그린 것이다.
그 필터 내에서는.. 수평으로 변화가 그닥 없을 것이다. 다 픽셀값이 비슷하기에!
그러면서 x축 값이 커질수록 필터가 커지겠고, 그럼 필터 끄트머리 쪽의 픽셀값이 점점 밝아지면서 변화량이 증가한다.
그러다가 변화량이 최고점을 찍으면 이것은 저 동그라미를 잘 포함한 필터가 될 것이다. 별 오차 없이!
이후 필터가 더 커지면.. 점점 변화량이 줄어든다.
왜냐면 일단 LoG filter는 가우시안 필터링 이후 Laplacian을 적용하는데, 흰부분이 많아지면 가우시안에서 너무 스무딩돼서 경계를 찾기가 어려워 특징을 감지할 수가 없기 때문이다.
그래서 결과적으로 저 그래프에서 가장 높은 값을 가지는 부분의 sigma가 특성을 추출하는 가장 적합한 sigma라는 것이다!
그럼 보통은, 여러 이미지가 있을 것이고 이미지마다의 크기도 다르고, 구별해내려는 객체의 크기도 다르기 때문에,
일단 내가 객체를 탐지하려는 부분에 크게 필터를 만들어놓는다.
전체 이미지에 LoG를 적용시킬 것인데, sigma값이 작은 것부터 시작한다.
작을 때 뭐 다른 부분에서 특징이 감지될 수도 있고, 아닐 수도 있다. 근데 이건 상관 없다.
sigma를 키우면서, 아까 만들어놓은 필터 안의 값 중 객체가 드러나는 부분이 생길 것이다.
이 이상 sigma를 키우면 그 객체는 덜 탐지되게 될 것이다.
이를 이용해서 적당한 sigma를 구한다.
이 과정은 이미지의 크기가 다른 경우와 객체의 크기가 다른 경우 등등, 다 따로 진행된다.
이 말은, 만약 같은 이미지여도 Full size VS 3/4 size라면, 3/4 size의 적절한 sigma와 Full size의 적절한 sigma는 다를 것이란 얘기다.
그리고 당연히 같은 이미지라면, 더 크기가 큰 이미지에서의 sigma가 더 클 것이다.
DoG
위의 LoG를, DoG로 대체하겠다.
DoG가 더 구하기 쉬우니깐!
아래 그림에서 빨강-노랑=파랑 이 식은 거의 성립하는 것처럼 보일 것이다.
그리고 -되는 부분, 즉 노란 부분의 sigma값이 빨간 부분의 sigma값보다 항상 커야 한다.
이를 이미지에 적용하면, sigma1 < sigma2일 때,
sigma1을 적용한 이미지에서 sigma2를 적용한 이미지를 빼면, 결과가 완성된다.
SIFT
Scale Invariant Feature Transform
SIFT는 탐지기와 묘사기 둘을 의미한다.
1) Scale-space extrema detection
LoG와 마찬가지로, DoG를 적용한 출력값이 커야 block일 확률이 높다.
만약 7*7 필터가 있다고 생각해보자. 그럼 이 필터를 통과한 결고는 7*7의 정보를 가져오는 것이다.
근데 이 필터의 sigma 값이 작아서.. 3*3 크기만큼만 유효해진다면? 정보를 그만큼밖에 못 가져오는 것이다.
그렇기 때문에 일단 이미지를 정한 후, 그 이미지에 sigma=a인 가우시안 필터를 통과시킨다.
그 출력 이미지에 또 sigma=a^2인 가우시안 필터를, 그 출력에 또 sigma=a^3인 필터를.. 이렇게 반복!
이 sigma는 1보다 작은 값이니 제곱할수록 작아진다.
이런 방식으로 sigma의 크기를 다양화시킨다.
그리고 각 출력 이미지를 빼준 것으로 DoG 결과물을 만든다.
결국 (G(sigma2)-G(sigma1))*I, (G(sigma3)-G(sigma2))*I... 이렇게 여럿 만들어질 것이다.
그리고 Image의 크기를 resize시켜 또 같은 과정을 반복한다.
sigma를 바꾸는 것과, Image size를 바꾸는 것. 이렇게 두 과정이 있는 것이다.
DoG 이미지의 극값(min or max)은 현재 및 인접 스케일에서 3*3 영역의 26개 이웃 픽셀과 비교하여 감지된다.
즉.. 본인 포함, 3*3*3 = 27개의 픽셀 중 극값을 찾는 것이다.
2) Keypoint localization
1. 일단 너무 낮은 응답 제거
x가 극값으로 탐지돼도, abs(D(x))가 threshold(0.03)보다 낮을 때 제거
2. 엣지 제거
- 2*2 행렬 계산, H = [Dxx Dxy \n Dxy Dyy]
- 최대고유값과 최소고유값의 비율 체크,
r = 최대고유값/최소고유값 이라고 정의하면, 아래 식을 정의할 수 있다.

그리고 여기서 r의 threshold는 10이다.
한 방향으로의 응답이 강한 엣지는 제거!
Origin -> DoG-> D(x) threshold -> edge threshold
Feature description
Q. 두 이미지를 어떻게 매칭시킬까?
- 각 이미지에서 흥미로운 점을 위 방식으로 포착.
- 서로 맞는 쌍을 찾는다. (이 단계를 할 것임 이제)
이게 어려운 이유는, 아무리 모든 게 같은 이미지여도 빛에 따라 변할 수가 있다.
그리고 뭐 각도나.. 위치가 다른 것도 있고 말이다.
만약.. 그 필터를 flatten 시킨다면, 어디서든.. 쓸데가 없다.
예를 들어 색이 달라진다면.. 픽셀값이 가지각색이기 때문이다.
절대 강도 값에 덜 민감하게 반응하려면 어떻게 해야 할까?
3*3 필터를 '차이'를 나타내는 벡터로 바꾸는 것이다.
ex) (1, 2)-(1,1) , (1, 3)-(1, 2), (2, 2)-(2, 1), (2, 3)-(2, 2), (3, 2)-(3, 1), (3, 3)-(3, 2)가 된다.. 아래 이미지를 참고!

이렇게 하면 절대 강도에는 덜 민감해진다. 근데 만약 이미지가 rotation이 있다거나 하면..? 이 관계도 깨져버린다.
Color Histogram
pixel의 값(밝기)을 히스토그램으로 만드는 것이다.
만약 pixel이 충분히 많으면 그냥 히스토그램, 데이터 수가 적어서 히스토그램이 많이 빈다면 bin을 통한 히스토그램으로!
이건 뭐 색이나 회전에 대한 변형에서는 자유로울 수 있다.
그치만.. 만약 픽셀값의 분포가 비슷한 이미지라면 둘의 구별이 쉽지 않을 것이다.

이런 식으로 말이다.
Spatial Histogram
이미지를 격자로 나누어 히스토그램을 여러 개 만드는 것.
이럼 공간 배치를 유지할 수도 있고, 변형에 대한 일정한 불변성이 있을 수 있다. (?)
Orientation Normalizaion
지배적인 기울기 방향에 따라 패치를 회전하는 것이다.
이렇게 하면 패치가 정방향으로 배치된다.
Orientation assignment
1. 규모에 따라, 키포인트 위치 주변에 이웃이 있다.
2. 그 영역에서 기울기 크기와 방향이 계산된다.
키포인트에 대한 가장 가까운 스케일을 가진 가우시안 평활 이미지가 어디있는가
Gradient orientations의 화살표 길이는 magnitude에 비례하며, 방향은 gradient 방향이다.

3. orientation 히스토그램을 만든다. (360도를 36개의 bin으로 커버하는)
- 기울기 크기(magnitude)와 가우시안에 의해, sigma가 있는 가중 원형 window에 의해 가중치 부여
- 보통 patch 크기는 16x16
- 위에서 말한 가우시안 가중치의 중심은 key point로 판별된 픽셀
4. 지배적인 방향을 추정한다.
- orientation에 대한 히스토그램에서 가장 높은 애를 고르고, 그의 80%(그냥 hyperparameter) 이상 되는 또다른 애들도 고른다.
이것들이 모두 orientation을 계산하는 데 고려된다.
- 이렇게 골라진 애들을 각각 주각도로 해서 바꾼 특징벡터를 v1, v2, v3... 이렇게 될 수 있다.
저 특징벡터들을 모두 사용해본다.
그럼 이제 어떻게 하느냐, 하면

왼쪽 사진은 변화가 많은 부분이 0도 에서 일 텐데, 오른쪽은 변화가 많은 부분이 45도라고 돼있다.
그럼 이걸 feature vector로 바꾸면 왼쪽은 [100 0 0 0 0...]', 오른쪽은 [0 0 0 0 100 0 0..]' 일 것이다.
이 둘의 차이는 매우 크다. 그럼 오른쪽의 45도를 0도가 되도록 회전하면 된다.
(구현상으로는 histogram을 다 밀면 된다)
keypoint descriptor
1. keypoint 주변 16*16 이웃 탐색
2. 이를 4*4 사이즈 16개로 나눔
3. 나눠진 각 sub-block을 orientation histogram으로 만드는데, 45도씩 나눠서 8개의 bin을 가진 히스토그램으로 만듦.
- 총 8*16=128개의 bin이 나옴
4. 히스토그램을 벡터로 표현해본다.
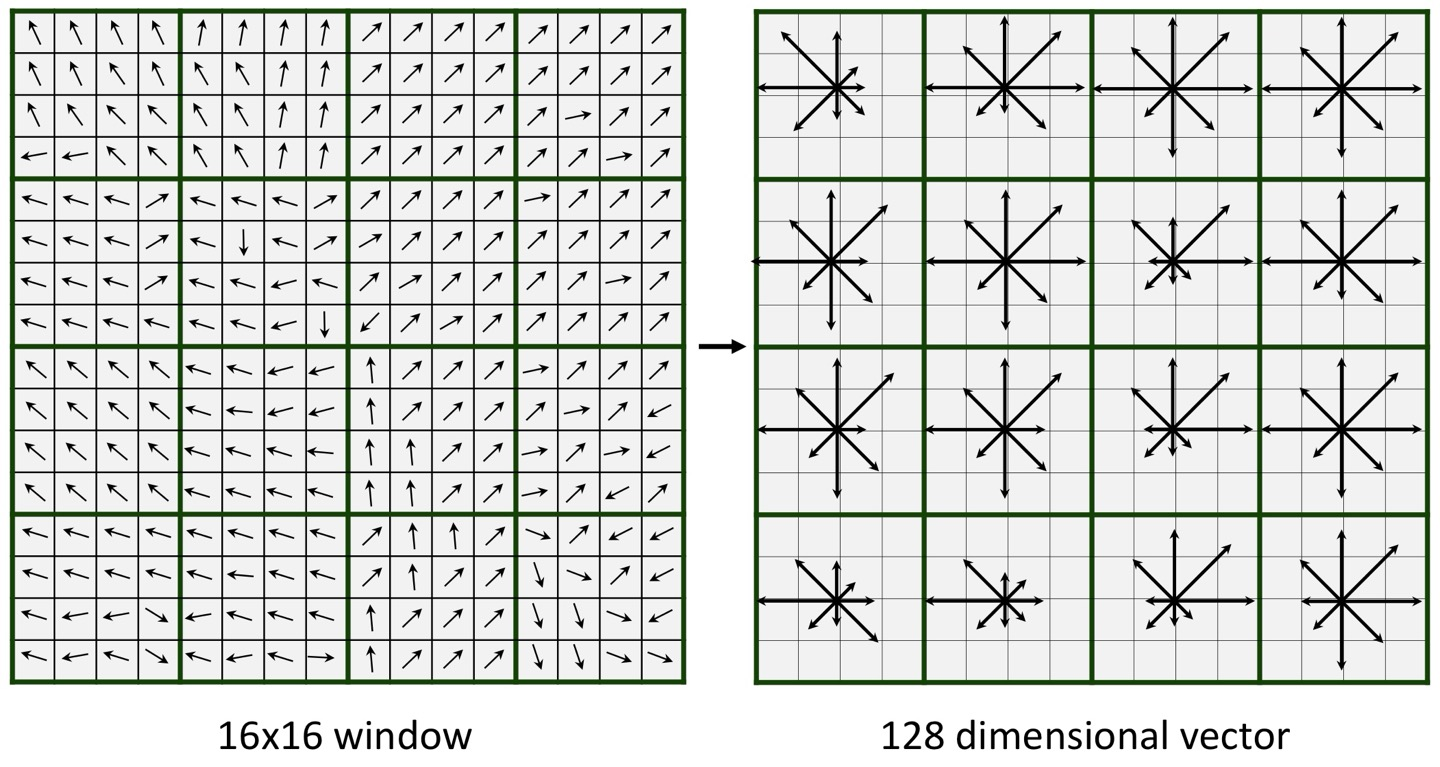
이렇게 되는 것이고~ 1행부터 4행까지 모든 window를 flatten시키면 128차원 벡터가 나온다.
SIFT의 속성
매우 견고한 매칭 기법임
- 관점 변화 처리 가능
- 조명의 큰 변화 처리 가능
- 빠르고 효율적
'AI > 컴퓨터비전' 카테고리의 다른 글
| Image Warping (new!) (0) | 2024.12.16 |
|---|---|
| Image Alignment (1) | 2024.12.16 |
| Image Classification (0) | 2024.12.15 |
| Image segmentation (3) | 2024.12.09 |
| CNN, Architectures (0) | 2024.12.09 |
