본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
다중 선형 회귀
feature가 여러 개인 것!
그리고 feature 수가 p개면 parameter 수는 p+1개. 회귀식에 상수항까지 있기 때문에 +1
모델링 과정은 전에도 말했듯,
1. 모델을 고르고, 2. 손실 함수를 고르고, 3. 모델을 적합시키고, 4. 모델 성능을 평가하면 된다.
보통 통계에선 1&2과정을 통틀어 OLS(Ordinary Least Squares)라 한다.
1. 모델 고르기
우선 이 데이터들을 벡터 형태로 나타낼 건데, 상수항까지 고려해서
y_hat = [1, x_1, x_2, ..., x_p] .T * [o_0, o_1, o_2, ..., o_p] 이렇게 나타낼 수 있다!
그리고 저 측정값들이 여러 개일 테니, 그들을 모두 합해서
y는 벡터, X는 행렬, parameter는 벡터로 나타낼 수 있다.
여기서 X같이 1열이 1벡터인 행렬을 디자인행렬이라 한다. (상수항 부분)
디자인 행렬의 각 열은 특성을 나타내고, 각 행은 관측치를 나타낸다.
따라서 (p+1)*n 행렬이다.
참고로 parameter vector는 (p+1, ), Prediction vector Y는 (n, )이다.
2. 손실 함수 고르기
norm이라는 것은 벡터의 크기의 측정인데,
n차원 벡터에 대한 L2 vector norm을 구하자면 루트 안에 제곱합을 넣으면 된다.
그럼 mse를 squared L2 norm이라 재정의할 수 있고,

이렇게 생각할 수 있다!
Ordinary Least Squares
이건 앞에서 말한 R을 최소화하는 파라미터를 찾는 문제라고 생각하면 된다.
일단 Yhat을 X*theta로 본다면, 이 OLS 문제를 세 가지 형태로 해석할 수 있는데,
1. 선형모델 Y_hat = X*theta의 mse를 최소화하는 문제,
2. 예측값 Y_hat과 실제값 Y의 거리를 최소화하는 문제,
3. 잔차 벡터 Y-Y_hat의 길이를 최소화하는 문제
이렇게 셋이다.
3. 모델 적합시키기
기하학적인 아이디어를 사용할 것인데, 우리는 어떻게 거리(잔차 벡터의 norm)를 최소화할까?
Y에 가장 가까운 span(X)의 벡터는 span(X)에 대한 Y의 직교 투영이다.
따라서, 우리는 잔차벡터가 span(X)에 직교하도록 하는 theta를 선택해야 한다.
least squares estimate theta_hat은 R을 최소화하는 파라미터이다.
동등하게, 이 theta_hat은 잔차벡터 Y-X*theta_hat이 span(X)에 직교하게 한다.

이 식은 갑자기 왜 나왔는진 모르겠지만 알아두자
4. 모델 평가하기
- 잔차플랏
좋은 잔차플랏은 패턴이 없는 플랏이다.
또한 전체 플랏에 걸쳐 비슷한 수직(세로) 산포를 갖는다. 만약 그렇지 않다면 예측의 정확도를 신뢰할 수 없다.
- 결정계수, R square
단순 선형 회귀에선 RMSE를 에러로, r을 두 변수 간 선형관계를 나타내는 측도인 표본상관계수로 쓴다.
다중 선형 회귀에선 RMSE를 에러로, R^2를 두 변수 간 선형관계를 나타내는 측도인 결정계수로 쓴다.
이 결정계수가 뭐냐하면, 적합된 값의 분산을 실제값의 분산으로 나눈 값이다.
이는 0~1 사이의 값이고, 모델이 설명하는 분산의 비율이라고 할 수 있다.
우리가 설명변수를 추가할수록 적합값은 실제값에 더욱 가까워져가고, 항상 결정계수는 오른다.
그치만 이 설명변수를 계속 추가한다고 해서 좋은 게 아니다. 과적합 될 수 있기에,
설명변수를 추가해도 결정계수가 큰 폭으로 증가하지 않는다면 설명변수의 추가를 멈춰야 한다.
결정계수는 이러한 문제가 있기에 수정된 결정계수를 사용하는 경우도 있다.
결정계수는 모델이 데이터를 얼마나 잘 나타내는가를 의미한다.
경사하강법, Gradient Descent
모델을 고르고 손실함수를 고르면, 모델의 손실을 최소화하도록 파라미터를 최적화한다.
어떻게 하냐면, 아까 위의 theta_hat 식을 사용하거나, 편미분해서 0이되는 부분을 찾으면 된다.
다른 손실함수를 가진 복잡한 모델을 디자인하기 위해선, 우리는 새로운 최적화 기술인 경사하강법이 필요한데,
이건 위처럼 식을 풀어서 정확한 답을 구하는 것 대신 알고리즘으로 접근하는 것이다.
일단 랜덤하게 아무 위치에서 추측을 시작한다.
기울기를 따라.. 그 점을 움직인다.
미분값이 다음 예측값을 말해준다. 예를 들어, 음수 기울기라면 점은 오른쪽으로, 양수 기울기라면 점은 왼쪽으로 움직인다.

결과적으로 이런 식을 따르게 되고, alpha는 만약 저 미분값이 너무 커서 x_t가 너무 많이 이동하게 될까봐 그걸 줄여주는 learning rate이다.
Convexity
convex한 함수일 땐, 어떠한 지역적 최솟값이더라도 전역적 최솟값이다.
그치만 non-convex할 땐.. 지역적 최솟값은 그저 지역적 최솟값에 머무는 경우가 대다수이다.
이 경사하강법 알고리즘은 단지 convex한 함수에 대해서만 최솟값을 찾을 수 있도록 보장한다.
1D Model에서의 경사 하강 알고리즘은,
모델은 y_hat = theta*x, 손실함수는 MSE로 한다면

이 식이

이렇게 표현된다. (L 편미분한 식을 대입한 것)
그럼 2D Model이나 그 이상 차원의 모델들은 다중선형회귀이며,
파라미터가 여럿이기에 loss surface를 고려해야 한다.
위에서는 그냥 하나의 식으로 나타내면 됐지만, 2D나 그 이상의 차원이라면 벡터로 나타내는 것이 좋다.
그리고 참고로, L의 편미분값에 -1을 곱하면 항상 최솟값 쪽을 향하게 된다.
1D든 2D든 그 이상이든 항상 local min에 도달했다면, 큰 비율로 뛰어넘어서 나갔다가 다시 GD 수행하면 좋다.
Mini-batch gradient descent
원래는 모든 데이터셋을 하나의 배치로 보고 미분값 계산을 수행하는데,
만약 데이터셋의 크기가 너무 큰 경우, 이 계산은 너무 오래 걸리고 개별 업뎃이 느려지기에
이에 대한 대안으로 전체 데이터셋을 미니배치로 나누어 경사하강법을 진행하는 방법이 있다.
batch size : 각 그룹의 데이터 개수, SGD에 비해 안정적으로 수렴한다.
보통 요즘 mini-batch stochastic gradient descent를 이거로 생각함.
Stochastic gradient descent
단 하나의 데이터 포인트의 배치 크기로 경사하강법 수행하기 때문에,
업데이트가 빠르다! 하지만 불안정하게 수렴한다.
분류(Classification)
범주형 변수에 대한 예측이다.
이진분류는 두 클래스, 0/1에 대해 예측한다.
다중분류는 많은 클래스에 대해 예측한다. 이미지 라벨링이나 다음 단어 등의 내용이다.
분류 중에는 Logistic Regression이 있다.
이름만 봐서 회귀라고 착각할 수도 있지만, 0/1로 나타내는 이진분류이다!
요건 예측값이 '확률'로, 0에서 1사이 값이고,
만약 예측값이 0.5 이상이면 1로, 이하면 0으로 예측한다.
여기선 theta_hat을 찾기 위해 모델을 최적화한다.
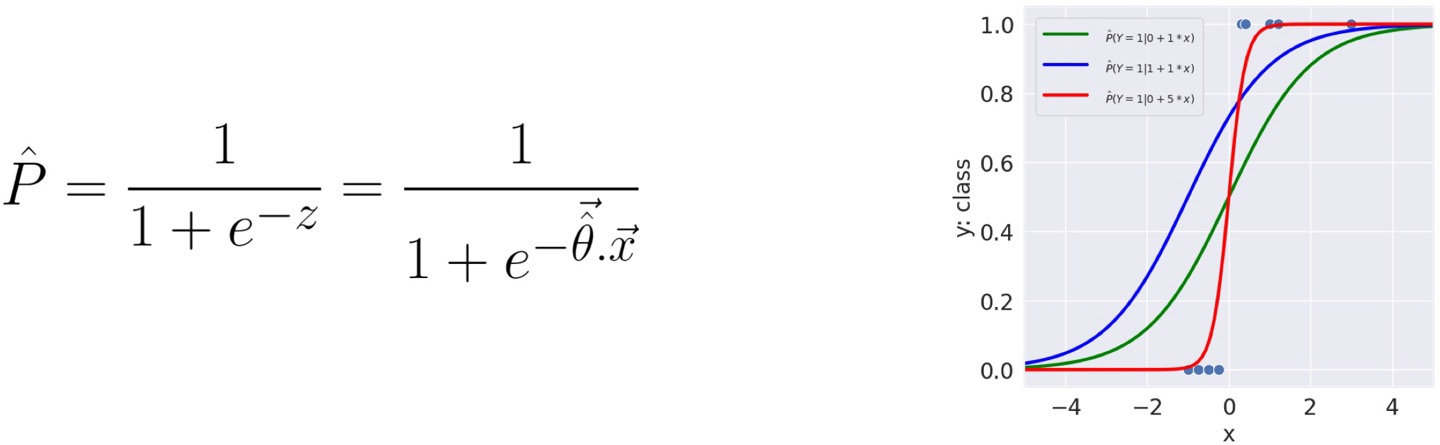

그럼 모델을 학습시키기 위해서 Loss가 필요한데,
이런 분류 문제에서는 보통 Cross-entropy Loss, CE Loss를 쓴다.
아래 식과 같이 정의된다.

그럼 y가 1일 땐 CE=-log(p), y가 0일 땐 CE=-log(1-p)가 된다.
앞에 붙어있는 - 는 Loss값을 양수로 만들기 위함이다.
그래프를 보면 y와 p에 따라 그래프가 어떻게 변화하는지 볼 수 있다.

Empirical Risk
Average Cross-Entropy Loss
- 하나의 데이터포인트에 대해, ce curve는 convex하다. 이건 전역적 최솟값을 가지고 있다.
- 그럼 저 평균 CE Loss라는 Empirical risk는 뭘까?
- 로지스틱 회귀에서, n개의 데이터에 대한 empirical risk는 다음과 같이, 모든 CE를 더하고 이를 n으로 나누어 사용한다.

- 그러므로 여기서 최적화 문제는 R(theta)를 최소화시키는 theta의 추정값을 찾는 것이 목표이다.
Linear Separability
- 입력인 x사이 두 클래스 y를 분리하는 초평면이 존재한다면 분류 데이터셋은 선형적으로 분리할 수 있다.
- 만약 하나의 특성이 있다면 input feature는 1dim이다.
- 당연히.. 클래스 라벨은 특성이 아니라 출력값으로 구분된다.
- 만약 x값에 대한 y값을 그래프로 나타냈을 때 이를 세로선으로 나눌 수 있다면 separable,
만약 두 feature에 대한 값을 그래프로 나타냈을 때 이를 선으로 분리할 수 있다면 separable! 아래 사진 참고

Linear separablity는 다양한 가중치를 만들어내는데, 일단 가장 간단한 로지스틱 회귀 모형을 적합해보자.
이럼 최적의 가중치 추정값은 -무한대가 된다.
이럼 모델은 과신하게 되고, 새로운 데이터에 대해 이상하게 예측하게 되고, log(0)이 -무한이 되기 때문에, Loss가 무한하게 돼서 추가 학습이 불가능하다.
가중치가 매우 커지는 것을 방지하기 위해 정규화를 쓴다.
원래는 argmin값이 무한지만, 정규화를 사용하면 argmin값이 유한해진다.
평가 메트릭
만약 메일이 스팸인지 햄인지 판별하는 문제가 있다면,
(spam = 1, ham = 0으로 할 것.)
진짜 스팸메일은 5개, 그냥 메일은 95개 였다고 하자.
Accuracy
분류문제에서 가장 좋은 메트릭은 아니다.
모든 메일을 ham이라고 예측했다면, 0.95의 정확도를 얻을 수 있을 것이다. 근데 여기선 spam을 하나도 탐지하지 못했다.
모든 메일을 spam이라고 예측했다면, 0.05의 정확도를 얻을 수 있다. 하지만 spam을 모두 탐지했다.
precision & recall
precision은 내가 탐지한 데이터 중 잘 한 비율, 즉

recall은 내가 탐지해야 하는 데이터 중 잘 한 비율, 즉

입력에 관계없이 분류기 출력을 '1'로 설정하면 recall이 100%이다.
왜냐면 내가 1을 찾아야 하는데 일단 1은 다 찾은 거니깐!
precision과 recall은 서로 trade-off 관계이다.
Confusion Matrix

AUC
area under curve
ROC curve와 PR curve 모두에 대한 다양한 AUC가 있는데, 보통 ROC가 더 흔히 쓰인다.
가장 좋은 AUC=1, 가장 안좋은 AUC=0.5이다.
보통 랜덤 예측을 하면 0.5가 나온다.
x축이 FP rate, y축이 TP rate이다.
'AI > 데이터과학' 카테고리의 다른 글
| Vector Space Model, TFIDF, Word2vec (68-70p 추가) (2) | 2024.12.13 |
|---|---|
| 결정트리(Decision Tree) (1) | 2024.12.12 |
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
| Association Rule Mining (0) | 2024.10.21 |
| 상관관계 분석과 가설 검정 (0) | 2024.10.21 |
본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
다중 선형 회귀
feature가 여러 개인 것!
그리고 feature 수가 p개면 parameter 수는 p+1개. 회귀식에 상수항까지 있기 때문에 +1
모델링 과정은 전에도 말했듯,
1. 모델을 고르고, 2. 손실 함수를 고르고, 3. 모델을 적합시키고, 4. 모델 성능을 평가하면 된다.
보통 통계에선 1&2과정을 통틀어 OLS(Ordinary Least Squares)라 한다.
1. 모델 고르기
우선 이 데이터들을 벡터 형태로 나타낼 건데, 상수항까지 고려해서
y_hat = [1, x_1, x_2, ..., x_p] .T * [o_0, o_1, o_2, ..., o_p] 이렇게 나타낼 수 있다!
그리고 저 측정값들이 여러 개일 테니, 그들을 모두 합해서
y는 벡터, X는 행렬, parameter는 벡터로 나타낼 수 있다.
여기서 X같이 1열이 1벡터인 행렬을 디자인행렬이라 한다. (상수항 부분)
디자인 행렬의 각 열은 특성을 나타내고, 각 행은 관측치를 나타낸다.
따라서 (p+1)*n 행렬이다.
참고로 parameter vector는 (p+1, ), Prediction vector Y는 (n, )이다.
2. 손실 함수 고르기
norm이라는 것은 벡터의 크기의 측정인데,
n차원 벡터에 대한 L2 vector norm을 구하자면 루트 안에 제곱합을 넣으면 된다.
그럼 mse를 squared L2 norm이라 재정의할 수 있고,

이렇게 생각할 수 있다!
Ordinary Least Squares
이건 앞에서 말한 R을 최소화하는 파라미터를 찾는 문제라고 생각하면 된다.
일단 Yhat을 X*theta로 본다면, 이 OLS 문제를 세 가지 형태로 해석할 수 있는데,
1. 선형모델 Y_hat = X*theta의 mse를 최소화하는 문제,
2. 예측값 Y_hat과 실제값 Y의 거리를 최소화하는 문제,
3. 잔차 벡터 Y-Y_hat의 길이를 최소화하는 문제
이렇게 셋이다.
3. 모델 적합시키기
기하학적인 아이디어를 사용할 것인데, 우리는 어떻게 거리(잔차 벡터의 norm)를 최소화할까?
Y에 가장 가까운 span(X)의 벡터는 span(X)에 대한 Y의 직교 투영이다.
따라서, 우리는 잔차벡터가 span(X)에 직교하도록 하는 theta를 선택해야 한다.
least squares estimate theta_hat은 R을 최소화하는 파라미터이다.
동등하게, 이 theta_hat은 잔차벡터 Y-X*theta_hat이 span(X)에 직교하게 한다.

이 식은 갑자기 왜 나왔는진 모르겠지만 알아두자
4. 모델 평가하기
- 잔차플랏
좋은 잔차플랏은 패턴이 없는 플랏이다.
또한 전체 플랏에 걸쳐 비슷한 수직(세로) 산포를 갖는다. 만약 그렇지 않다면 예측의 정확도를 신뢰할 수 없다.
- 결정계수, R square
단순 선형 회귀에선 RMSE를 에러로, r을 두 변수 간 선형관계를 나타내는 측도인 표본상관계수로 쓴다.
다중 선형 회귀에선 RMSE를 에러로, R^2를 두 변수 간 선형관계를 나타내는 측도인 결정계수로 쓴다.
이 결정계수가 뭐냐하면, 적합된 값의 분산을 실제값의 분산으로 나눈 값이다.
이는 0~1 사이의 값이고, 모델이 설명하는 분산의 비율이라고 할 수 있다.
우리가 설명변수를 추가할수록 적합값은 실제값에 더욱 가까워져가고, 항상 결정계수는 오른다.
그치만 이 설명변수를 계속 추가한다고 해서 좋은 게 아니다. 과적합 될 수 있기에,
설명변수를 추가해도 결정계수가 큰 폭으로 증가하지 않는다면 설명변수의 추가를 멈춰야 한다.
결정계수는 이러한 문제가 있기에 수정된 결정계수를 사용하는 경우도 있다.
결정계수는 모델이 데이터를 얼마나 잘 나타내는가를 의미한다.
경사하강법, Gradient Descent
모델을 고르고 손실함수를 고르면, 모델의 손실을 최소화하도록 파라미터를 최적화한다.
어떻게 하냐면, 아까 위의 theta_hat 식을 사용하거나, 편미분해서 0이되는 부분을 찾으면 된다.
다른 손실함수를 가진 복잡한 모델을 디자인하기 위해선, 우리는 새로운 최적화 기술인 경사하강법이 필요한데,
이건 위처럼 식을 풀어서 정확한 답을 구하는 것 대신 알고리즘으로 접근하는 것이다.
일단 랜덤하게 아무 위치에서 추측을 시작한다.
기울기를 따라.. 그 점을 움직인다.
미분값이 다음 예측값을 말해준다. 예를 들어, 음수 기울기라면 점은 오른쪽으로, 양수 기울기라면 점은 왼쪽으로 움직인다.

결과적으로 이런 식을 따르게 되고, alpha는 만약 저 미분값이 너무 커서 x_t가 너무 많이 이동하게 될까봐 그걸 줄여주는 learning rate이다.
Convexity
convex한 함수일 땐, 어떠한 지역적 최솟값이더라도 전역적 최솟값이다.
그치만 non-convex할 땐.. 지역적 최솟값은 그저 지역적 최솟값에 머무는 경우가 대다수이다.
이 경사하강법 알고리즘은 단지 convex한 함수에 대해서만 최솟값을 찾을 수 있도록 보장한다.
1D Model에서의 경사 하강 알고리즘은,
모델은 y_hat = theta*x, 손실함수는 MSE로 한다면

이 식이

이렇게 표현된다. (L 편미분한 식을 대입한 것)
그럼 2D Model이나 그 이상 차원의 모델들은 다중선형회귀이며,
파라미터가 여럿이기에 loss surface를 고려해야 한다.
위에서는 그냥 하나의 식으로 나타내면 됐지만, 2D나 그 이상의 차원이라면 벡터로 나타내는 것이 좋다.
그리고 참고로, L의 편미분값에 -1을 곱하면 항상 최솟값 쪽을 향하게 된다.
1D든 2D든 그 이상이든 항상 local min에 도달했다면, 큰 비율로 뛰어넘어서 나갔다가 다시 GD 수행하면 좋다.
Mini-batch gradient descent
원래는 모든 데이터셋을 하나의 배치로 보고 미분값 계산을 수행하는데,
만약 데이터셋의 크기가 너무 큰 경우, 이 계산은 너무 오래 걸리고 개별 업뎃이 느려지기에
이에 대한 대안으로 전체 데이터셋을 미니배치로 나누어 경사하강법을 진행하는 방법이 있다.
batch size : 각 그룹의 데이터 개수, SGD에 비해 안정적으로 수렴한다.
보통 요즘 mini-batch stochastic gradient descent를 이거로 생각함.
Stochastic gradient descent
단 하나의 데이터 포인트의 배치 크기로 경사하강법 수행하기 때문에,
업데이트가 빠르다! 하지만 불안정하게 수렴한다.
분류(Classification)
범주형 변수에 대한 예측이다.
이진분류는 두 클래스, 0/1에 대해 예측한다.
다중분류는 많은 클래스에 대해 예측한다. 이미지 라벨링이나 다음 단어 등의 내용이다.
분류 중에는 Logistic Regression이 있다.
이름만 봐서 회귀라고 착각할 수도 있지만, 0/1로 나타내는 이진분류이다!
요건 예측값이 '확률'로, 0에서 1사이 값이고,
만약 예측값이 0.5 이상이면 1로, 이하면 0으로 예측한다.
여기선 theta_hat을 찾기 위해 모델을 최적화한다.
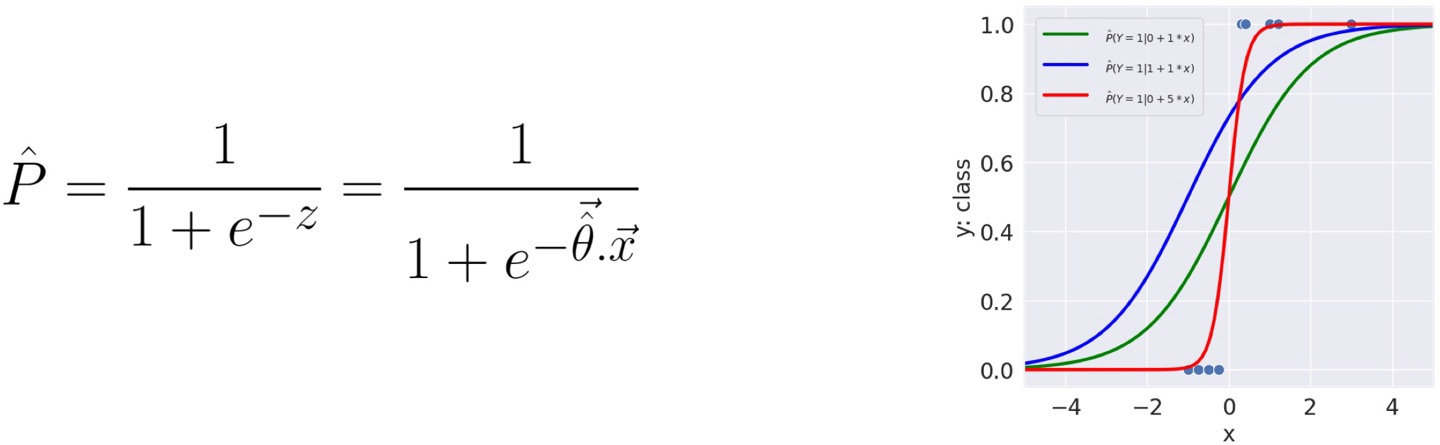

그럼 모델을 학습시키기 위해서 Loss가 필요한데,
이런 분류 문제에서는 보통 Cross-entropy Loss, CE Loss를 쓴다.
아래 식과 같이 정의된다.

그럼 y가 1일 땐 CE=-log(p), y가 0일 땐 CE=-log(1-p)가 된다.
앞에 붙어있는 - 는 Loss값을 양수로 만들기 위함이다.
그래프를 보면 y와 p에 따라 그래프가 어떻게 변화하는지 볼 수 있다.

Empirical Risk
Average Cross-Entropy Loss
- 하나의 데이터포인트에 대해, ce curve는 convex하다. 이건 전역적 최솟값을 가지고 있다.
- 그럼 저 평균 CE Loss라는 Empirical risk는 뭘까?
- 로지스틱 회귀에서, n개의 데이터에 대한 empirical risk는 다음과 같이, 모든 CE를 더하고 이를 n으로 나누어 사용한다.

- 그러므로 여기서 최적화 문제는 R(theta)를 최소화시키는 theta의 추정값을 찾는 것이 목표이다.
Linear Separability
- 입력인 x사이 두 클래스 y를 분리하는 초평면이 존재한다면 분류 데이터셋은 선형적으로 분리할 수 있다.
- 만약 하나의 특성이 있다면 input feature는 1dim이다.
- 당연히.. 클래스 라벨은 특성이 아니라 출력값으로 구분된다.
- 만약 x값에 대한 y값을 그래프로 나타냈을 때 이를 세로선으로 나눌 수 있다면 separable,
만약 두 feature에 대한 값을 그래프로 나타냈을 때 이를 선으로 분리할 수 있다면 separable! 아래 사진 참고

Linear separablity는 다양한 가중치를 만들어내는데, 일단 가장 간단한 로지스틱 회귀 모형을 적합해보자.
이럼 최적의 가중치 추정값은 -무한대가 된다.
이럼 모델은 과신하게 되고, 새로운 데이터에 대해 이상하게 예측하게 되고, log(0)이 -무한이 되기 때문에, Loss가 무한하게 돼서 추가 학습이 불가능하다.
가중치가 매우 커지는 것을 방지하기 위해 정규화를 쓴다.
원래는 argmin값이 무한지만, 정규화를 사용하면 argmin값이 유한해진다.
평가 메트릭
만약 메일이 스팸인지 햄인지 판별하는 문제가 있다면,
(spam = 1, ham = 0으로 할 것.)
진짜 스팸메일은 5개, 그냥 메일은 95개 였다고 하자.
Accuracy
분류문제에서 가장 좋은 메트릭은 아니다.
모든 메일을 ham이라고 예측했다면, 0.95의 정확도를 얻을 수 있을 것이다. 근데 여기선 spam을 하나도 탐지하지 못했다.
모든 메일을 spam이라고 예측했다면, 0.05의 정확도를 얻을 수 있다. 하지만 spam을 모두 탐지했다.
precision & recall
precision은 내가 탐지한 데이터 중 잘 한 비율, 즉

recall은 내가 탐지해야 하는 데이터 중 잘 한 비율, 즉

입력에 관계없이 분류기 출력을 '1'로 설정하면 recall이 100%이다.
왜냐면 내가 1을 찾아야 하는데 일단 1은 다 찾은 거니깐!
precision과 recall은 서로 trade-off 관계이다.
Confusion Matrix

AUC
area under curve
ROC curve와 PR curve 모두에 대한 다양한 AUC가 있는데, 보통 ROC가 더 흔히 쓰인다.
가장 좋은 AUC=1, 가장 안좋은 AUC=0.5이다.
보통 랜덤 예측을 하면 0.5가 나온다.
x축이 FP rate, y축이 TP rate이다.
'AI > 데이터과학' 카테고리의 다른 글
| Vector Space Model, TFIDF, Word2vec (68-70p 추가) (2) | 2024.12.13 |
|---|---|
| 결정트리(Decision Tree) (1) | 2024.12.12 |
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
| Association Rule Mining (0) | 2024.10.21 |
| 상관관계 분석과 가설 검정 (0) | 2024.10.21 |
