본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
'상관관계'라고 하면 데이터간 관계가 있음을 나타내는 말이라고 생각할 것이다.
이걸 좀 자세히 다뤄보겠다.
Correlation, 상관분석
상관계수는 어떻게 쓰이냐면,
두 수치형 변수간 관계를 측정하고 묘사하며,
한 변수가 변하면 나머지 변수도 변한다.
그치만 인과관계라고 할 수는 없고, 공변량이다. (공유하는 변화량 이라고 생각하면 된다.)
가장 흔히 쓰이는 상관계수는 피어슨 상관계수이다.
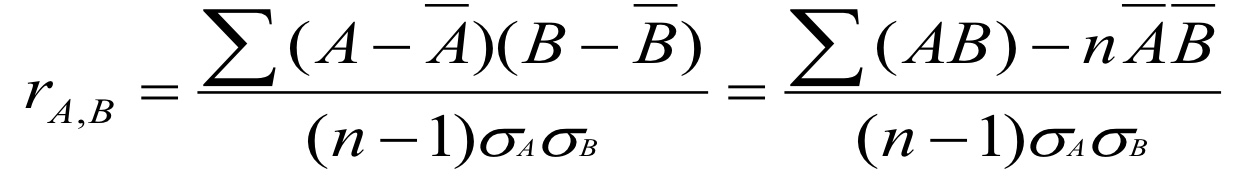
이렇게 계산하는 것이고, n은 데이터의 개수, 알파벳 위의 _는 bar라고 읽으며 그 알파벳으로 나타내진 데이터의 평균을 의미한다.
분모에 있는 동그랗게 생긴 기호는 sigma이고, 데이터의 표준편차를 나타낸다. 표준편차의 제곱이 분산이다.
두 변수가 정규분포를 따른다고 가정한 식이다.
상관계수의 의미를 간단히 말하자면,
r이 1에 가까울 수록 비례 관계, -1에 가까울 수록 반비례 관계, 0에 가까울 수록 관계가 없음을 의미한다.
보통 r의 절댓값이 0.5보다 크다면 어느정도 관계가 있다고 본다.
그리고 r의 절댓값이 0에서 0.3 사이라면 관계가 약하다고 본다.
추정
상관분석은 추정을 해야 하는데, 5가지를 살펴보아야 한다.
1. 변수를 측정할 때 간격 또는 비율 수준에서 변수를 측정해야 한다.
2. 선형 관계라고 가정한다. 선형관계는 산점도를 직선으로 나타낼 수 있는 데이터를 말하며, 각 변수를 편미분했을 때 편미분한 변수가 식에 남지 않으면 선형관계이다. 예를 들어, y = x는 x로 미분하면 x가 안 남으므로 선형관계이고, y = x^2은 x로 미분하면 x가 남으므로 비선형 관계이다.
3. 또, 두 변수는 정규분포를 따른다고 가정하는데, 이를 확인하려면 히스토그램을 그리거나, Q-Q plot을 그리거나, 통계 검정을 시행하면 된다.
4. 이상치가 없다고 가정해야 한다. 극단이상치가 있는 경우는 상관계수의 값이 엄청나게 감소하게 된다.
5. 데이터 쌍이 맞아야 한다. 양쪽 데이터 모두 존재해야 하고, 같은 개체에서 추출된 데이터여야 한다. 또한 관찰이 독립적으로 이루어진 변수여야 한다.
공분산, Covariance
공분산은 상관계수와 비슷하다. 공분산의 식과, 상관계수와의 관계는 아래와 같다.
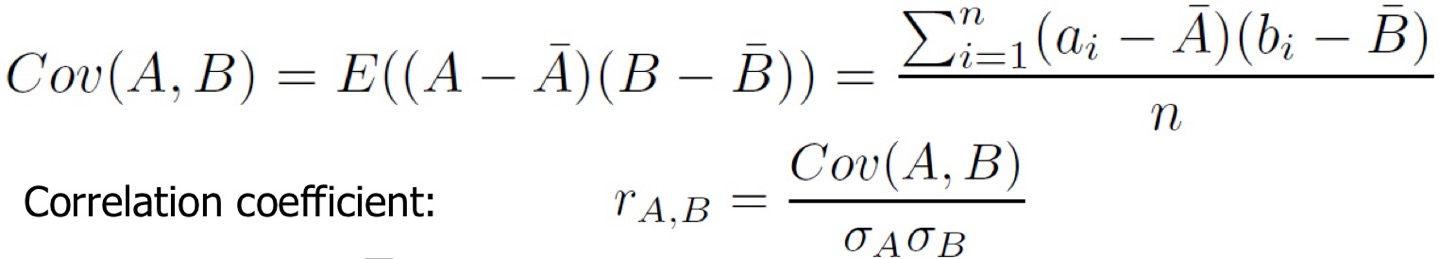
이 식을 쉽게 구하려면, E(AB)-bar(A)*bar(B)를 구해도 똑같은 결과가 나온다.
공분산이 0보다 크다면, A와 B는 모두 기댓값보다 큰 경향을 가지고 있고,
공분산이 0보다 작다면, A와 B는 반비례 기댓값을 가지고 있다.
또한 독립이라면 공분산이 0이지만, 공분산이 0이라고 모두 독립인 건 아니다.
가설 검정
검정이라는 말이 생소하게 느껴질 텐데, 그냥 확인하는 거라고 생각하면 된다.
가설이 맞는지를 확인하는 것이다. 이건 유의성 검정이라고도 한다.
우선 그럼 가설을 세워야할 텐데, 가설이라는 것은 '모집단에 대한 내용을 파라미터로 예측하는 것'이다.
보통 검정은 샘플 데이터 추정치와 가설에 의해 예측된 값을 비교해서 검정하는 형식이다.
가설이 사실이라면 우리가 얻은 데이터와 같은 데이터를 가질 가능성이 낮은가를 말한다.
아직까진 이해가 어렵겠지만, 차근차근 단계를 밟아보겠다.
[유의성 검정의 5단계]
1. 확인
- 데이터 타입이 뭔지, 샘플링 방법은 랜덤으로 했는지, 모집단의 분포는 어떤지, 샘플 사이즈는 충분히 큰지
2. 가설 세우기
가설은 두 개를 세우는데, 귀무 가설과 대립 가설이다.
보통 내가 기각하고 싶은 걸 귀무가설로 세운다. 귀무가설과 대립가설은 서로 반대된다.(겹치면 안됨!)
예를 들어 귀무가설 H_0를 '평균이 170이다'로 세웠다면, 대립가설 H_a는 '평균이 170보다 크다'(한쪽검정) 또는 '평균이 170이 아니다'(양쪽검정)으로 세울 수 있다.
3. 검정 통계량
- 가설 검정에서 사용된 샘플 데이터로부터 계산된 랜덤 변수
4. P-value(p값)
- 귀무가설의 증거에 대한 확률. p값이 작을 수록 귀무가설을 더 강하게 기각할 수 있다.
5. 결론
- 만약 아직 결정이 필요하지 않다면, p-값을 이용해 결과를 작성하면 되고,
- 결정이 필요하다면, 임계값과 p-값을 비교해서 가설을 기각하거나 말거나를 정하면 된다.
<단계>
우선 귀무가설과 대립가설을 세우고,
임계값인 alpha를 설정한다.
검정 통계량을 계산한 후,
alpha를 이용해 기각역을 설정한다.
p-값을 결정하고,
결과를 구할 땐 두 가지 방법이 있는데,
1) alpha과 p-값을 비교해, 귀무가설을 기각할지 결정한다.
2) 또는 검정통계량과 기각역을 비교해, 귀무가설을 기각할지 결정한다.
검정통계량, Test Statistic
그럼 위에서 말한 검정 통계량이 도대체 뭔지 궁금할 것이다.
여기선 주로 사용하는 Z-통계량에 대해 얘기하겠다.
이건 모집단의 분포가 정규분포를 따른다고 가정할 수 있고, 분산이 알려져 있을 때 쓸 수 있는 방법이다.
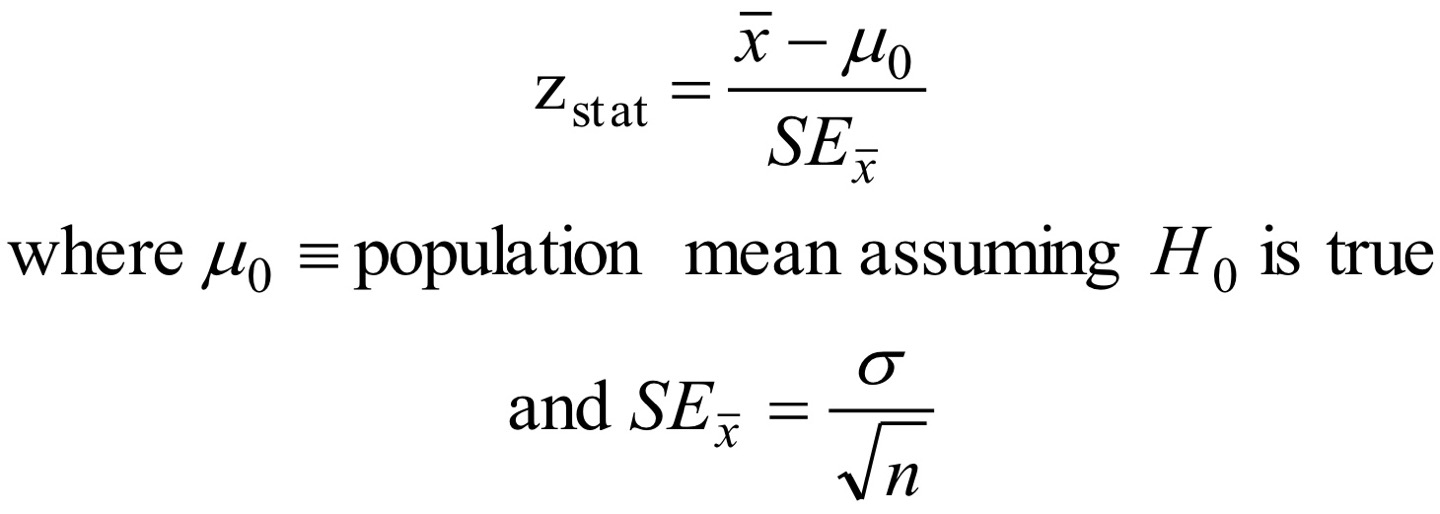
이 검정통계량으로 p-value도 계산할 수 있고, 만약 양측검정이라면 p값이 두 배가 된다.
p값으로 귀무가설을 기각할 수 있는 정도를 알아보자면,
0.05에서 1사이는 어느정도 유의하고, 0.01에서 0.05사이면 유의하고, 0.01보다 작으면 엄청 유의하다.
이 Z-검정을 쓰려면 조건이 있는데,
분산을 알아야 하고,
모집단이 정규근사거나 표본 수가 크고,
표본이 랜덤하게 뽑히고,
유효한 데이터이고,
표준편차가 알려지지 않은 경우 샘플의 크기가 30이상이어야 한다.
'AI > 데이터과학' 카테고리의 다른 글
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
|---|---|
| Association Rule Mining (0) | 2024.10.21 |
| EDA의 일부, 데이터 전처리와 특성 추출 (2) | 2024.10.19 |
| 데이터 시각화 (1) | 2024.10.19 |
| 정규표현식 (Regular Expression) (0) | 2024.10.19 |
본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
'상관관계'라고 하면 데이터간 관계가 있음을 나타내는 말이라고 생각할 것이다.
이걸 좀 자세히 다뤄보겠다.
Correlation, 상관분석
상관계수는 어떻게 쓰이냐면,
두 수치형 변수간 관계를 측정하고 묘사하며,
한 변수가 변하면 나머지 변수도 변한다.
그치만 인과관계라고 할 수는 없고, 공변량이다. (공유하는 변화량 이라고 생각하면 된다.)
가장 흔히 쓰이는 상관계수는 피어슨 상관계수이다.
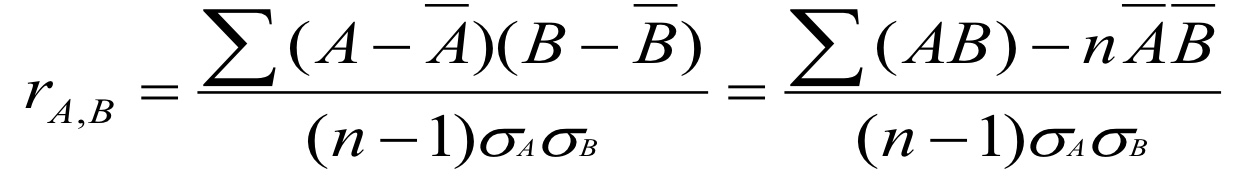
이렇게 계산하는 것이고, n은 데이터의 개수, 알파벳 위의 _는 bar라고 읽으며 그 알파벳으로 나타내진 데이터의 평균을 의미한다.
분모에 있는 동그랗게 생긴 기호는 sigma이고, 데이터의 표준편차를 나타낸다. 표준편차의 제곱이 분산이다.
두 변수가 정규분포를 따른다고 가정한 식이다.
상관계수의 의미를 간단히 말하자면,
r이 1에 가까울 수록 비례 관계, -1에 가까울 수록 반비례 관계, 0에 가까울 수록 관계가 없음을 의미한다.
보통 r의 절댓값이 0.5보다 크다면 어느정도 관계가 있다고 본다.
그리고 r의 절댓값이 0에서 0.3 사이라면 관계가 약하다고 본다.
추정
상관분석은 추정을 해야 하는데, 5가지를 살펴보아야 한다.
1. 변수를 측정할 때 간격 또는 비율 수준에서 변수를 측정해야 한다.
2. 선형 관계라고 가정한다. 선형관계는 산점도를 직선으로 나타낼 수 있는 데이터를 말하며, 각 변수를 편미분했을 때 편미분한 변수가 식에 남지 않으면 선형관계이다. 예를 들어, y = x는 x로 미분하면 x가 안 남으므로 선형관계이고, y = x^2은 x로 미분하면 x가 남으므로 비선형 관계이다.
3. 또, 두 변수는 정규분포를 따른다고 가정하는데, 이를 확인하려면 히스토그램을 그리거나, Q-Q plot을 그리거나, 통계 검정을 시행하면 된다.
4. 이상치가 없다고 가정해야 한다. 극단이상치가 있는 경우는 상관계수의 값이 엄청나게 감소하게 된다.
5. 데이터 쌍이 맞아야 한다. 양쪽 데이터 모두 존재해야 하고, 같은 개체에서 추출된 데이터여야 한다. 또한 관찰이 독립적으로 이루어진 변수여야 한다.
공분산, Covariance
공분산은 상관계수와 비슷하다. 공분산의 식과, 상관계수와의 관계는 아래와 같다.
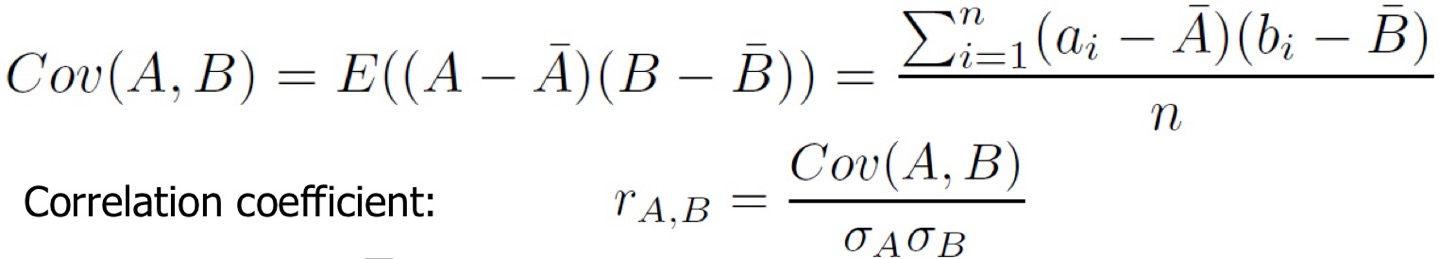
이 식을 쉽게 구하려면, E(AB)-bar(A)*bar(B)를 구해도 똑같은 결과가 나온다.
공분산이 0보다 크다면, A와 B는 모두 기댓값보다 큰 경향을 가지고 있고,
공분산이 0보다 작다면, A와 B는 반비례 기댓값을 가지고 있다.
또한 독립이라면 공분산이 0이지만, 공분산이 0이라고 모두 독립인 건 아니다.
가설 검정
검정이라는 말이 생소하게 느껴질 텐데, 그냥 확인하는 거라고 생각하면 된다.
가설이 맞는지를 확인하는 것이다. 이건 유의성 검정이라고도 한다.
우선 그럼 가설을 세워야할 텐데, 가설이라는 것은 '모집단에 대한 내용을 파라미터로 예측하는 것'이다.
보통 검정은 샘플 데이터 추정치와 가설에 의해 예측된 값을 비교해서 검정하는 형식이다.
가설이 사실이라면 우리가 얻은 데이터와 같은 데이터를 가질 가능성이 낮은가를 말한다.
아직까진 이해가 어렵겠지만, 차근차근 단계를 밟아보겠다.
[유의성 검정의 5단계]
1. 확인
- 데이터 타입이 뭔지, 샘플링 방법은 랜덤으로 했는지, 모집단의 분포는 어떤지, 샘플 사이즈는 충분히 큰지
2. 가설 세우기
가설은 두 개를 세우는데, 귀무 가설과 대립 가설이다.
보통 내가 기각하고 싶은 걸 귀무가설로 세운다. 귀무가설과 대립가설은 서로 반대된다.(겹치면 안됨!)
예를 들어 귀무가설 H_0를 '평균이 170이다'로 세웠다면, 대립가설 H_a는 '평균이 170보다 크다'(한쪽검정) 또는 '평균이 170이 아니다'(양쪽검정)으로 세울 수 있다.
3. 검정 통계량
- 가설 검정에서 사용된 샘플 데이터로부터 계산된 랜덤 변수
4. P-value(p값)
- 귀무가설의 증거에 대한 확률. p값이 작을 수록 귀무가설을 더 강하게 기각할 수 있다.
5. 결론
- 만약 아직 결정이 필요하지 않다면, p-값을 이용해 결과를 작성하면 되고,
- 결정이 필요하다면, 임계값과 p-값을 비교해서 가설을 기각하거나 말거나를 정하면 된다.
<단계>
우선 귀무가설과 대립가설을 세우고,
임계값인 alpha를 설정한다.
검정 통계량을 계산한 후,
alpha를 이용해 기각역을 설정한다.
p-값을 결정하고,
결과를 구할 땐 두 가지 방법이 있는데,
1) alpha과 p-값을 비교해, 귀무가설을 기각할지 결정한다.
2) 또는 검정통계량과 기각역을 비교해, 귀무가설을 기각할지 결정한다.
검정통계량, Test Statistic
그럼 위에서 말한 검정 통계량이 도대체 뭔지 궁금할 것이다.
여기선 주로 사용하는 Z-통계량에 대해 얘기하겠다.
이건 모집단의 분포가 정규분포를 따른다고 가정할 수 있고, 분산이 알려져 있을 때 쓸 수 있는 방법이다.
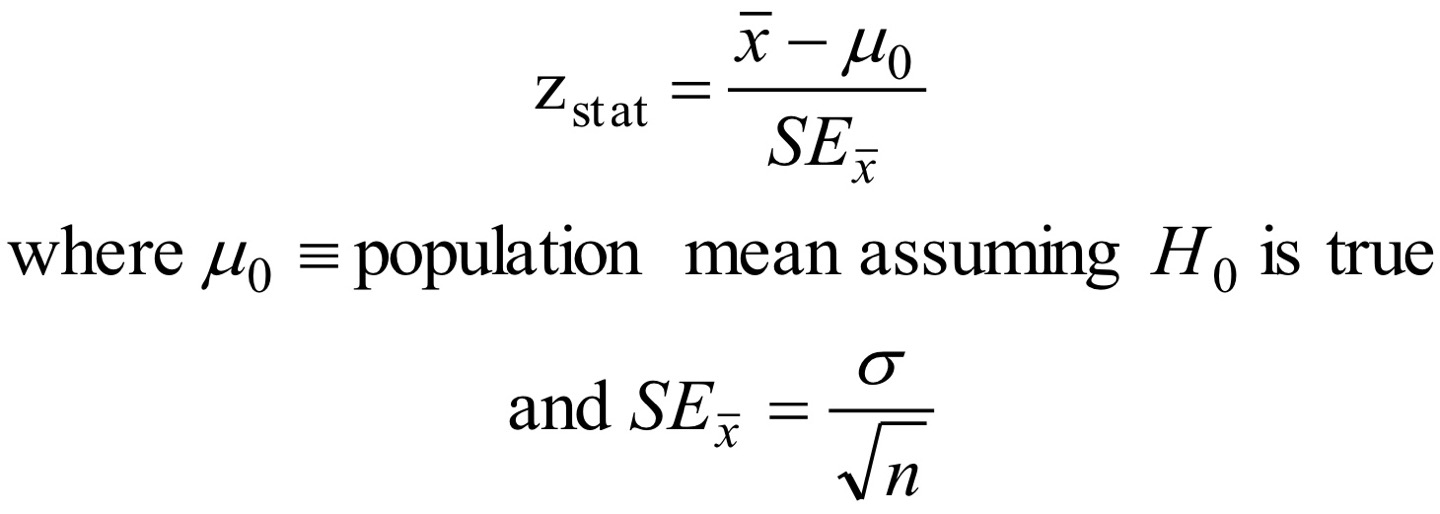
이 검정통계량으로 p-value도 계산할 수 있고, 만약 양측검정이라면 p값이 두 배가 된다.
p값으로 귀무가설을 기각할 수 있는 정도를 알아보자면,
0.05에서 1사이는 어느정도 유의하고, 0.01에서 0.05사이면 유의하고, 0.01보다 작으면 엄청 유의하다.
이 Z-검정을 쓰려면 조건이 있는데,
분산을 알아야 하고,
모집단이 정규근사거나 표본 수가 크고,
표본이 랜덤하게 뽑히고,
유효한 데이터이고,
표준편차가 알려지지 않은 경우 샘플의 크기가 30이상이어야 한다.
'AI > 데이터과학' 카테고리의 다른 글
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
|---|---|
| Association Rule Mining (0) | 2024.10.21 |
| EDA의 일부, 데이터 전처리와 특성 추출 (2) | 2024.10.19 |
| 데이터 시각화 (1) | 2024.10.19 |
| 정규표현식 (Regular Expression) (0) | 2024.10.19 |
