본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
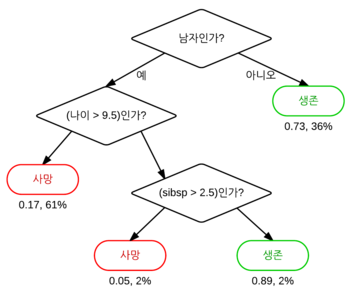
되게 간단하게 분류하는 모델이다.
질문에 대한 답변으로 분류하는 것!
예를 들어,
동물인가요? yes
다리가 몇 개인가요? 2
무슨색인가요? white
요런식으로.. 분류함!
이제부터는 이 결정트리에 대해 Iris flower data set을 이용해볼 것이다.
여기서 설명변수는 petal length, petal width, sepal length, sepal width가 있다.
그리고 목표는 다른 데이터에 대해 종을 구별해내는 것이다. target = species(versicolor, setosa, virginica)
단지 분포표만을 보고도 dt를 생성할 수 있다.
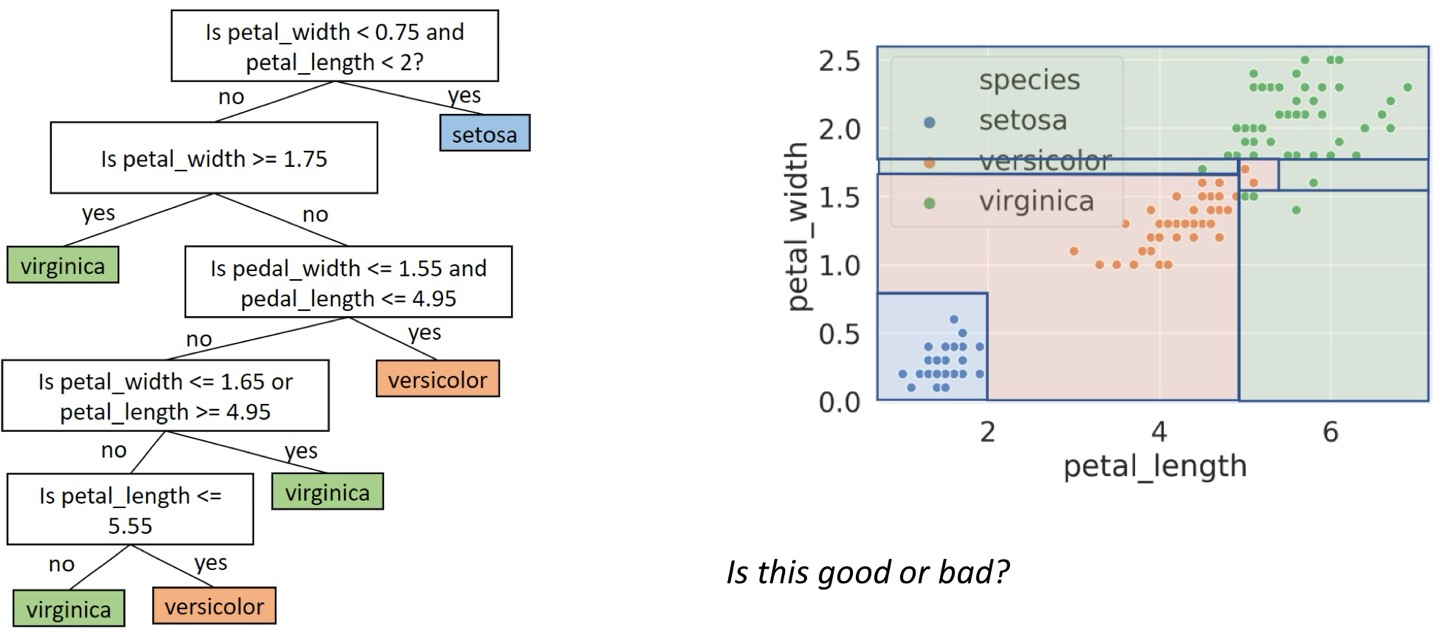
이렇게 말이다.
위처럼 non-linear하게 나타낼 수 있어서 logistic regression같은 linear로만 나타낸 모델보다 정확도가 높다.
그럼 과적합 되지 않을까 하는 의문이 들 수 있는데,
어떻게든 모델을 짜면 항상 100%의 정확도를 얻을 수 있기에.. 과적합 가능성이 있다.
위의 오른쪽 그림은 petal_length와 petal_width에 대한 것으로, 2개의 변수이기에 2차원으로 나타낼 수 있다.
근데 만약 다른 변수도 추가하고 싶다면? 이렇게 그림으로 나타내기는 어렵다. 뭐 성능은 나쁘지 않을 것이다.
물론 왼쪽처럼은 나타낼 수 있다.
이 과적합의 문제는.. 아래와 같은 그림처럼 나타난다. 이 그림처럼 된 모델의 accuracy는 0.7밖에 안 된다.
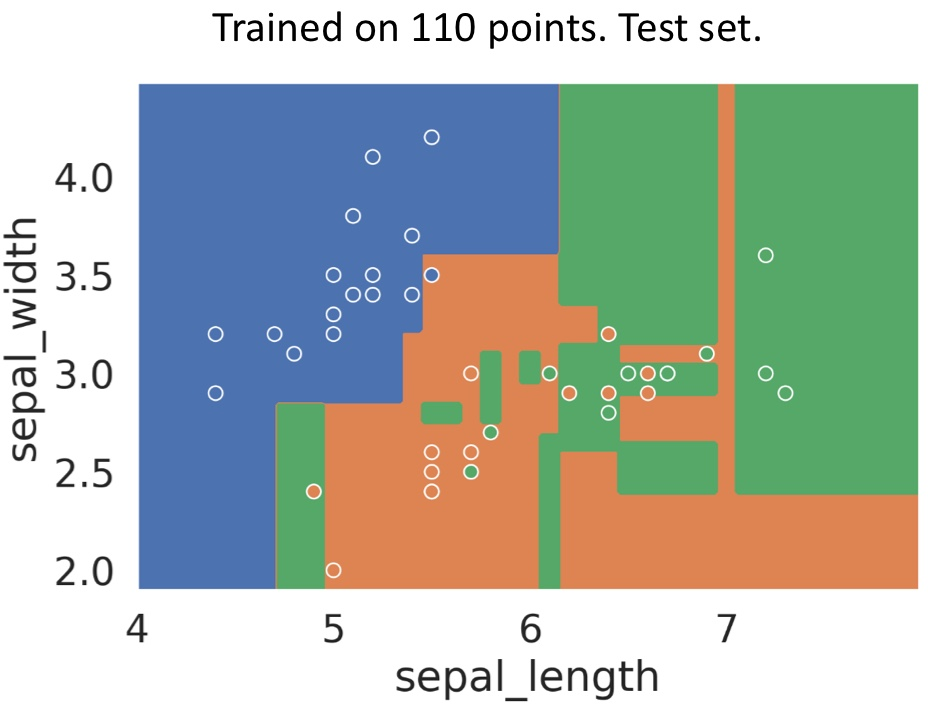
엄청 복잡해 보이기도 하고.. 이럼 진짜 과적합 된다.
Decision Tree Generation
전통적인 dt generation 알고리즘은,
모든 데이터가 root 노드에서 시작해서, 각 노드가 pure하거나 분리불가능할 때까지 반복한다.
pure : 하나의 유형만 있는 노드
unplittable : 분할 불가능한 중복 데이터가 있는 노드
위에서 나눈 것처럼 데이터를 분리하려는데, 가로선을 그을지 세로선을 그을지 정해야 한다.
잘 나누면 한 방에 pure한 부분이 생긴다.
예를 들어 이렇게 말이다!
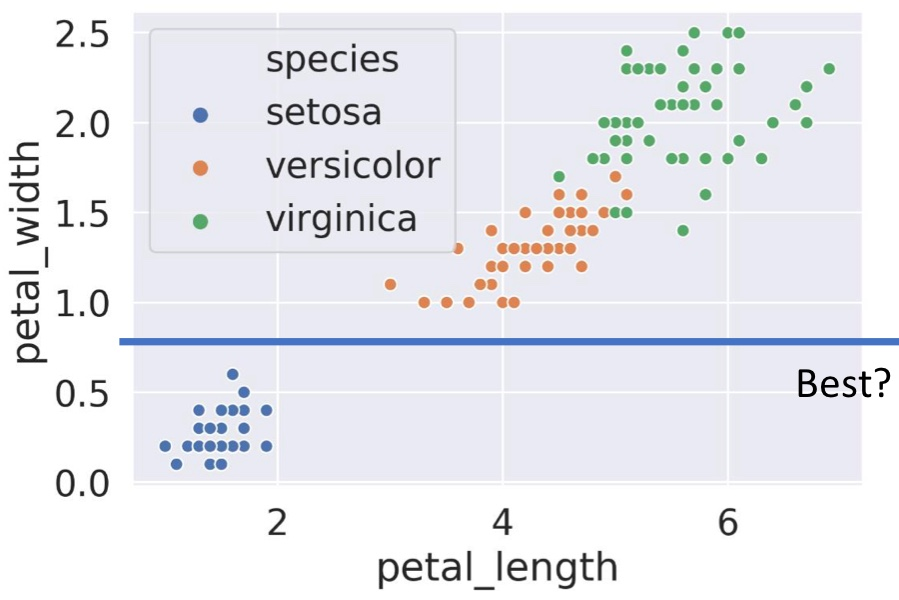
Node Entropy
[루트노드 예시]
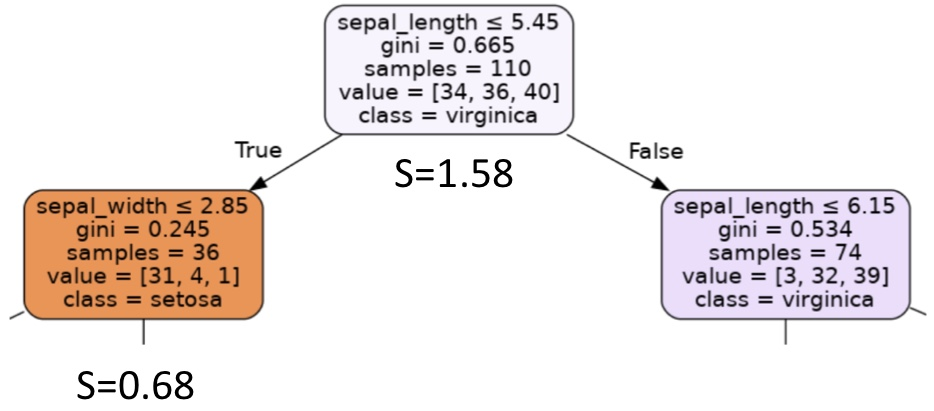
일단 루트노드를 보자. 나눠야 하는 클래스가 3개이고, 각 클래스의 데이터 개수는 [34, 36, 40]으로 주어진다. (value참고)
이 노드의 불확실성은, 각 클래스의 데이터 수가 비슷하므로 예측 가능성이 낮다 라고 판별하게 되는 것이다.
수치로 계산을 해보면, 데이터 비율은 p0=34/110=0.31, p1=0.33, p2=0.36이 되고,
이를 엔트로피로 표현해보면, 엔트로피 식은 S=-sigma(pc*log_2(pc))이므로,
S = -0.31*log_2(0.31)-0.33log_2(0.33)-0.36log_2(0.36)=0.52+0.53+0.53=1.58이 된다.
[자식노드 예시]
이것만 봐선 엔트로피가 높은 건지 낮은 건지.. 생각하기가 어려울 것이다.
그럼 왼쪽 자식 노드를 봐보자. 여기서 각 클래스의 데이터 개수는 [31, 4, 1]로, 첫 클래스인 데이터가 많고 나머지 데이터는 적은 것을 볼 수 있다.
여기서도 엔트로피를 계산해보면, 일단 각 클래스별 확률은 p0=0.86, p1=0.11, p2=0.028이 나온다.
여기서부터 확률을 보면.. 첫 번째 데이터의 비율이 가장 높다는 것을 알 수 있다.
그럼 엔트로피를 위의 식처럼 계산해보면 0.68이라는 값이 나온다.
[결과, 일반화]
결론적으로 이 엔트로피는, 엔트로피가 낮다면 예측 가능성이 높고, 엔트로피가 높다면 예측 가능성이 낮다는 말이다.
왼쪽 자식 노드는 엔트로피가 낮다. 그럼 예측 가능성이 높다. 그냥 p0클래스일 것이다 라고 예측하면 예측의 정확도가 0.86이니까 말이다.
따라서 루트노드처럼 데이터가 여러 클래스에 균등하게 분포된다면 엔트로피는 높아진다.
이 엔트로피에 대한 내용을 관찰해보자면,
1. 하나의 클래스에 대한 데이터만 있는 노드는 S=0
2. 두 클래스에 데이터가 균등하게 분포된 노드는 S=2*(-0.5*log_2(0.5))=1
3. 세 클래스에 데이터가 균등하게 분포된 노드는 S=3*(-0.33*log_2(0.33))=1.58
4. C개의 클래스에 균등하게 분포된 노드는 S=C*(-1/C*log_2(1/C))= - log_2(1/C)=log_2(C)
이렇게 일반화를 시켜볼 수 있다.
그렇다면 결정트리에서는, 이 엔트로피를 '최소화'하는 노드가 중요할 것이다.
그럼 분할했을 때 엔트로피가 최소화되는 노드를 구하기 위해 '가중치 엔트로피'를 사용할 수 있다. 이건 손실함수로도 쓰인다.
그 식은 아래와 같다. 여기서 S(X)는 X에 대한 엔트로피를 의미한다.
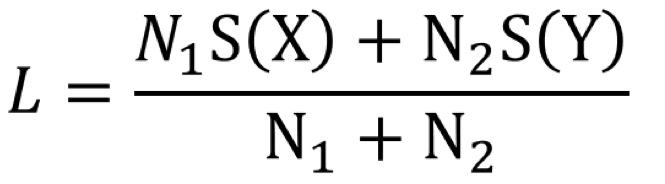
저 가중치는 어떻게 사용되냐면, 실제 예시를 봐보겠다.
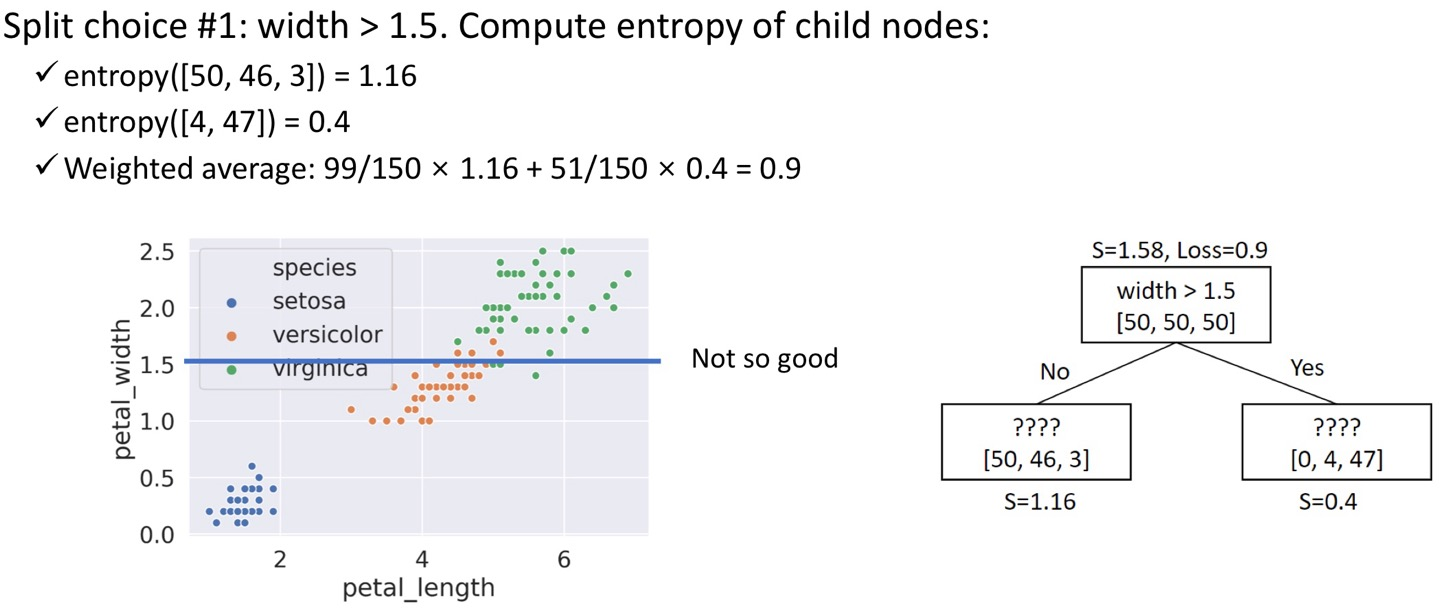
이게 뭐냐면, petal_width가 1.5보다 큰가? 라는 조건을 걸었을 때의 엔트로피를 계산해보는 과정이다.
루트노드를 보면 총 데이터는 [50, 50, 50]으로 세 클래스에 데이터가 균등하게 분포돼있는 것을 볼 수 있다.
근데 만약 width>1.5라는 기준을 통해 데이터를 분리해보면,
윗부분에서는 두 개의 클래스 데이터만 있고, [4, 47]로 데이터가 나뉜다. 그럼 이때의 엔트로피는 0.4라는 것이다.
아랫부분에서는 세 개의 클래스 데이터가 모두 있고, [50, 46, 3]으로 나뉘며, 엔트로피는 1.16이 된다.
그럼 위에 나온 가중치 엔트로피를 사용해 계산하면,
(4+47)/(50+50+50) * 0.4 + (50+46+3)/(50+50+50) * 1.16 이고, 이 값은 0.9이다.
이런식으로 기준을 정하고, 결과적으로 나뉘는 데이터를 보고 이렇게 엔트로피를 계산하면 된다.
이 예시에서는 petal_length에 대한 기준을 주기도 하고, petal_width에 대한 기준을 바꿔보기도 하면서 가장 낮은 가중치 엔트로피를 가지는 기준선을 찾게 된다.
전통적인 DT 알고리즘은, 위에서 말한 내용을 다시 상기시키자면,
루트 노드에서 시작해서, 모든 노드가 pure하거나 unsplittable할 때까지 반복하는 것이라고 했다.
이때 각 노드에서는 최적의 특징 x와, 분할 값 beta를 선택하게 된다.
그럼 이제 과적합을 방지하는 법에 대해 알아보겠다.
Overfitting
위에서도 말했듯 완전히 성장한 트리는 과적합 발생 가능성이 매우 높다. 일반화 능력이 부족할 수도 있단 것이다.
따라서 여기서 제안할 수 있는 과적합 방지 기법은,
1. 트리 성장을 제한하는 것
노드 깊이를 제한하거나, 데이터 포인트가 적은 노드는 분할을 금지하는등 트리가 무한히 성장하지 않도록 하는 것이다.
조금 자세히는, 샘플 수가 threshold 이하인 노드는 분할하지 않거나, 트리 최대 깊이가 7 이하이도록.. 하는 것이다.
2. Pruning, 가지치기
이건 일단 트리를 완전히 성장시킨 다음, 필요 없는 가지를 제거하는 것이다.
validation set을 사용해서 유용성이 낮은 노드를 판단한다. 그 노드를 가장 빈번한 클래스 혹은 평균값으로 대체해도 validation error가 증가하지 않는다면? 유용하지 않으니 해당 노드를 제거하는 것이다.
3. 랜덤 포레스트! 이건 더 간단하면서도 강력하다.
랜덤포레스트
위의 결정 트리를 많이 생성한 후, 그 트리들끼리 '다수결 투표'를 진행하는 것이다.
각 트리는 독립적으로 학습되기에, 랜덤 포레스트 모델의 편향은 낮지만, 분산은 크다.
근데 그럼 문제가 있는데, 우리는 하나의 트레이닝 셋만 있는데 여기서 어떻게 다양한 모델을..? 내지..?
Bagging
데이터의 부트스트랩 샘플(재표본)을 사용해서 여러 트리를 학습시킬 수 있다.
최종 모델은 각 작은 모델의 평균 예측값이 된다.
근데 그렇다고 해서 모델의 분산을 줄이는 것에 그렇게 효율적인 것은 아니다.
강렬한 feature가 있다면.. 그게 항상 쓰일 것이기 때문이다.
그렇다면 여기서 아이디어로, 각 분할 과정에서, m feature 중 표본만을 사용하는 것이다.
m=sqrt(p)로 보통 쓰인다. p는 feature의 개수이다.
이런 방식으로 하면 개별 트리가 생겼을 때, 이는 제각각으로 과적합 됐을 것이다.
그래도 여기서 원하는 것은, 전체적인 모델은 낮은 분산을 갖는 것이다.
랜덤 포레스트 알고리즘
각 노드에서 임의로 m개의 특성을 선택한다.
가중치 엔트로피를 최소화하는 가장 좋은 특성인 x와 가장 좋은 나누는 값인 beta를 고른다.
예측하기 위해, T개의 결정트리에 물어보고 다수결 투표를 진행한다.
이 접근법을 위해선 T와 m이라는 파라미터가 필요하다.
휴리스틱으로 과적합 피하기
크기/깊이 제한,
불필요 가지 제거,
트리 앙상블로 과적합 완화
-> 최적이 아니라 경험적 방식임.
-> 대신, 누가 해봤을 때 이거 좋다고 밝혀지긴 함.
장점은,
분류/회귀 모두에 사용할 수 있고,
특징 스케일링이 필요하지 않으며,
중요 특성을 자동으로 식별할 수 있고,
비선형 관계를 처리해서 복잡한 특징 엔지니어링이 필요하지 않고,
과적합 가능성이 낮다.
위의 내용은 모두 트리의 '분류'에 대한 내용이었는데,
이제 회귀에 대해서도 똑같이 진행해보겠다.
선형 모델 대신 회귀 트리를 만드는 것이다.
트리 모델 in 회귀
단지 두 개의 수정만을 가지고, 우리는 dt 모델을 회귀에 사용할 수 있다.
1. 조건 나누기 : MSE로 측정된 모델의 예측 정확도를 향상시키기 위한 분할 기준을 선택하고자 한다.
- 분할할 예측 변수 j를 선택하고 새로운 영역의 가중 평균 MSE가 가장 최소가 되도록 분할할 t_j(임계값)을 고른다.
-> 원랜 엔트로피가 최소화되도록 분할했는데, 여기선 MSE를 줄이는 방향으로 분할한다.
<목적 함수>
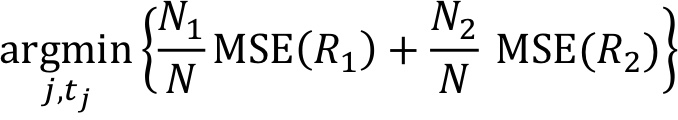
또는
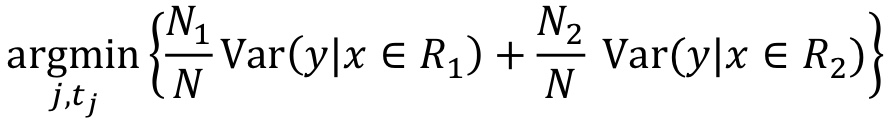
Ni는 Ri의 훈련 포인트 개수이고, N은 R의 포인트 개수이다.
분할 후, 두 영역에서의 평균 오차를 '최소화'하도록 분할값과 특성 선택하도록 함.
R에서 회귀분석을 위해 모델의 각 영역에 실수(해당영역 학습지점 출력값의 평균)를 라벨링하고자 함.
예를 들어,
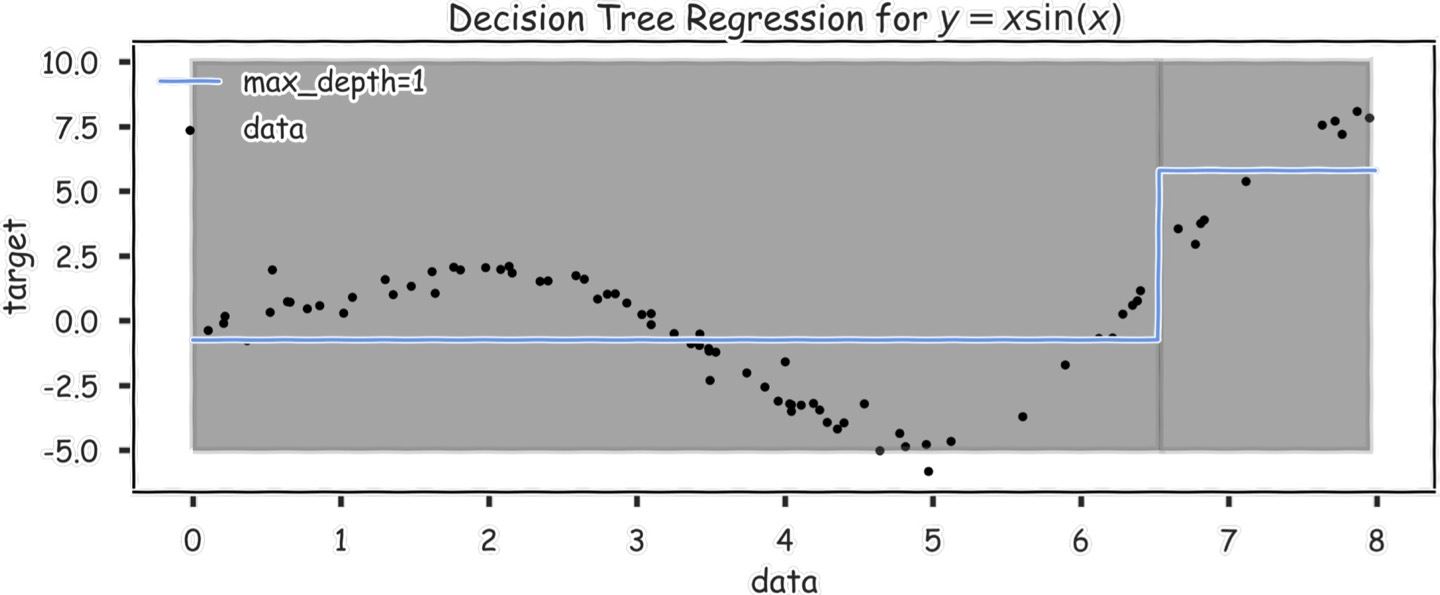
이렇게 한 6.5 정도에서 기준선이 있고,
그 전후 데이터들의 평균값이 저 파란 선이 된다.
max_depth=1인 것은, node가 하나라는 것이고, 위 그래프에서는 x<6.5 인 node 하나만 있다고 생각하면 된다.
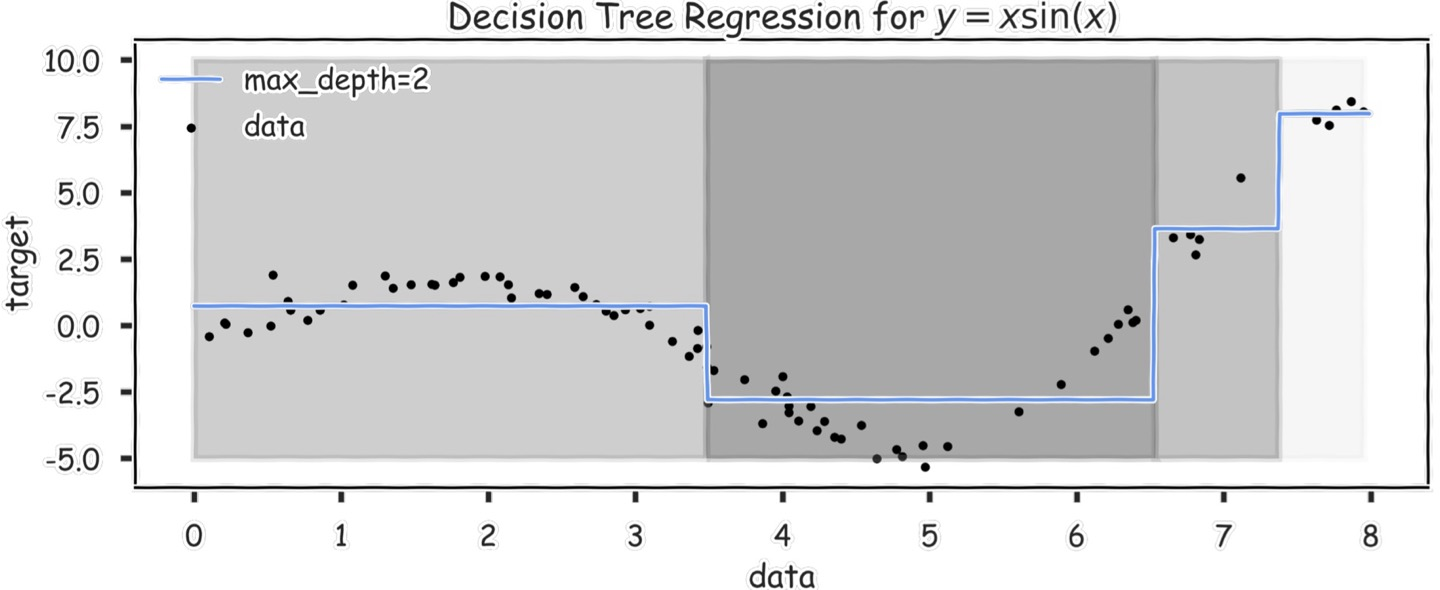
이 그래프에서는, max_depth=2라고 돼있는데, 그럼 node가 3개인 것이다.
루트노드는 x<6.5, 자식노드는 각각 x<3.5, x<7.4 정도의 내용일 것이다.
요런식으로 계속 진행하면.. 노드 수를 계속 증가시키면.. 다 쪼개서 평균을 구할 수 있을 것이다.
그럼 진짜 무슨 함수처럼 된다. 근데 그럼 당연히 과적합될 것이다.
여기서도 과적합을 방지하기 위해 조건들이 필요하다.
Stopping Conditions
최대 깊이 혹은 각 부분의 최소 포인트 개수에 도달한 경우,
순수 이득 대신, R 영역을 분할하는 정확도 이득을 계산할 수 있다.
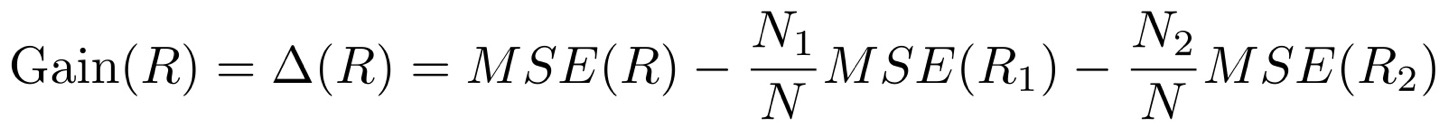
이 Gain은 에러가 얼마나 감소했는지에 대한 측도이고, 만약 gain이 특정 임계값보다 작다면 트리를 멈춘다.
그리고 MSE 대신 RSS(Residual sum of squares)를 사용할 수 있다.
결정트리는,
데이터를 선형으로 제한하지 않고, 분류 과정의 해석이 용이하다.
그렇지만 과적합 될 확률이 높고, 수학적으로 그다지 좋진 않다.
Boosting은 생략하겟어요~ㅎ
'AI > 데이터과학' 카테고리의 다른 글
| NN(Neural Networks), Convolution, Pooling (0) | 2024.12.14 |
|---|---|
| Vector Space Model, TFIDF, Word2vec (68-70p 추가) (2) | 2024.12.13 |
| 회귀/분류 (1) | 2024.12.10 |
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
| Association Rule Mining (0) | 2024.10.21 |
본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.

되게 간단하게 분류하는 모델이다.
질문에 대한 답변으로 분류하는 것!
예를 들어,
동물인가요? yes
다리가 몇 개인가요? 2
무슨색인가요? white
요런식으로.. 분류함!
이제부터는 이 결정트리에 대해 Iris flower data set을 이용해볼 것이다.
여기서 설명변수는 petal length, petal width, sepal length, sepal width가 있다.
그리고 목표는 다른 데이터에 대해 종을 구별해내는 것이다. target = species(versicolor, setosa, virginica)
단지 분포표만을 보고도 dt를 생성할 수 있다.

이렇게 말이다.
위처럼 non-linear하게 나타낼 수 있어서 logistic regression같은 linear로만 나타낸 모델보다 정확도가 높다.
그럼 과적합 되지 않을까 하는 의문이 들 수 있는데,
어떻게든 모델을 짜면 항상 100%의 정확도를 얻을 수 있기에.. 과적합 가능성이 있다.
위의 오른쪽 그림은 petal_length와 petal_width에 대한 것으로, 2개의 변수이기에 2차원으로 나타낼 수 있다.
근데 만약 다른 변수도 추가하고 싶다면? 이렇게 그림으로 나타내기는 어렵다. 뭐 성능은 나쁘지 않을 것이다.
물론 왼쪽처럼은 나타낼 수 있다.
이 과적합의 문제는.. 아래와 같은 그림처럼 나타난다. 이 그림처럼 된 모델의 accuracy는 0.7밖에 안 된다.

엄청 복잡해 보이기도 하고.. 이럼 진짜 과적합 된다.
Decision Tree Generation
전통적인 dt generation 알고리즘은,
모든 데이터가 root 노드에서 시작해서, 각 노드가 pure하거나 분리불가능할 때까지 반복한다.
pure : 하나의 유형만 있는 노드
unplittable : 분할 불가능한 중복 데이터가 있는 노드
위에서 나눈 것처럼 데이터를 분리하려는데, 가로선을 그을지 세로선을 그을지 정해야 한다.
잘 나누면 한 방에 pure한 부분이 생긴다.
예를 들어 이렇게 말이다!

Node Entropy

[루트노드 예시]
일단 루트노드를 보자. 나눠야 하는 클래스가 3개이고, 각 클래스의 데이터 개수는 [34, 36, 40]으로 주어진다. (value참고)
이 노드의 불확실성은, 각 클래스의 데이터 수가 비슷하므로 예측 가능성이 낮다 라고 판별하게 되는 것이다.
수치로 계산을 해보면, 데이터 비율은 p0=34/110=0.31, p1=0.33, p2=0.36이 되고,
이를 엔트로피로 표현해보면, 엔트로피 식은 S=-sigma(pc*log_2(pc))이므로,
S = -0.31*log_2(0.31)-0.33log_2(0.33)-0.36log_2(0.36)=0.52+0.53+0.53=1.58이 된다.
[자식노드 예시]
이것만 봐선 엔트로피가 높은 건지 낮은 건지.. 생각하기가 어려울 것이다.
그럼 왼쪽 자식 노드를 봐보자. 여기서 각 클래스의 데이터 개수는 [31, 4, 1]로, 첫 클래스인 데이터가 많고 나머지 데이터는 적은 것을 볼 수 있다.
여기서도 엔트로피를 계산해보면, 일단 각 클래스별 확률은 p0=0.86, p1=0.11, p2=0.028이 나온다.
여기서부터 확률을 보면.. 첫 번째 데이터의 비율이 가장 높다는 것을 알 수 있다.
그럼 엔트로피를 위의 식처럼 계산해보면 0.68이라는 값이 나온다.
[결과, 일반화]
결론적으로 이 엔트로피는, 엔트로피가 낮다면 예측 가능성이 높고, 엔트로피가 높다면 예측 가능성이 낮다는 말이다.
왼쪽 자식 노드는 엔트로피가 낮다. 그럼 예측 가능성이 높다. 그냥 p0클래스일 것이다 라고 예측하면 예측의 정확도가 0.86이니까 말이다.
따라서 루트노드처럼 데이터가 여러 클래스에 균등하게 분포된다면 엔트로피는 높아진다.
이 엔트로피에 대한 내용을 관찰해보자면,
1. 하나의 클래스에 대한 데이터만 있는 노드는 S=0
2. 두 클래스에 데이터가 균등하게 분포된 노드는 S=2*(-0.5*log_2(0.5))=1
3. 세 클래스에 데이터가 균등하게 분포된 노드는 S=3*(-0.33*log_2(0.33))=1.58
4. C개의 클래스에 균등하게 분포된 노드는 S=C*(-1/C*log_2(1/C))= - log_2(1/C)=log_2(C)
이렇게 일반화를 시켜볼 수 있다.
그렇다면 결정트리에서는, 이 엔트로피를 '최소화'하는 노드가 중요할 것이다.
그럼 분할했을 때 엔트로피가 최소화되는 노드를 구하기 위해 '가중치 엔트로피'를 사용할 수 있다. 이건 손실함수로도 쓰인다.
그 식은 아래와 같다. 여기서 S(X)는 X에 대한 엔트로피를 의미한다.
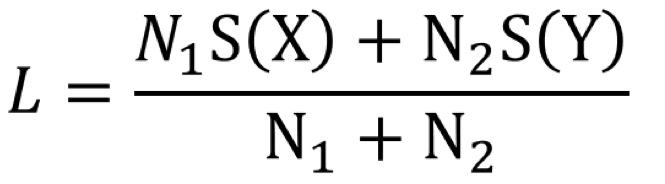
저 가중치는 어떻게 사용되냐면, 실제 예시를 봐보겠다.

이게 뭐냐면, petal_width가 1.5보다 큰가? 라는 조건을 걸었을 때의 엔트로피를 계산해보는 과정이다.
루트노드를 보면 총 데이터는 [50, 50, 50]으로 세 클래스에 데이터가 균등하게 분포돼있는 것을 볼 수 있다.
근데 만약 width>1.5라는 기준을 통해 데이터를 분리해보면,
윗부분에서는 두 개의 클래스 데이터만 있고, [4, 47]로 데이터가 나뉜다. 그럼 이때의 엔트로피는 0.4라는 것이다.
아랫부분에서는 세 개의 클래스 데이터가 모두 있고, [50, 46, 3]으로 나뉘며, 엔트로피는 1.16이 된다.
그럼 위에 나온 가중치 엔트로피를 사용해 계산하면,
(4+47)/(50+50+50) * 0.4 + (50+46+3)/(50+50+50) * 1.16 이고, 이 값은 0.9이다.
이런식으로 기준을 정하고, 결과적으로 나뉘는 데이터를 보고 이렇게 엔트로피를 계산하면 된다.
이 예시에서는 petal_length에 대한 기준을 주기도 하고, petal_width에 대한 기준을 바꿔보기도 하면서 가장 낮은 가중치 엔트로피를 가지는 기준선을 찾게 된다.
전통적인 DT 알고리즘은, 위에서 말한 내용을 다시 상기시키자면,
루트 노드에서 시작해서, 모든 노드가 pure하거나 unsplittable할 때까지 반복하는 것이라고 했다.
이때 각 노드에서는 최적의 특징 x와, 분할 값 beta를 선택하게 된다.
그럼 이제 과적합을 방지하는 법에 대해 알아보겠다.
Overfitting
위에서도 말했듯 완전히 성장한 트리는 과적합 발생 가능성이 매우 높다. 일반화 능력이 부족할 수도 있단 것이다.
따라서 여기서 제안할 수 있는 과적합 방지 기법은,
1. 트리 성장을 제한하는 것
노드 깊이를 제한하거나, 데이터 포인트가 적은 노드는 분할을 금지하는등 트리가 무한히 성장하지 않도록 하는 것이다.
조금 자세히는, 샘플 수가 threshold 이하인 노드는 분할하지 않거나, 트리 최대 깊이가 7 이하이도록.. 하는 것이다.
2. Pruning, 가지치기
이건 일단 트리를 완전히 성장시킨 다음, 필요 없는 가지를 제거하는 것이다.
validation set을 사용해서 유용성이 낮은 노드를 판단한다. 그 노드를 가장 빈번한 클래스 혹은 평균값으로 대체해도 validation error가 증가하지 않는다면? 유용하지 않으니 해당 노드를 제거하는 것이다.
3. 랜덤 포레스트! 이건 더 간단하면서도 강력하다.
랜덤포레스트
위의 결정 트리를 많이 생성한 후, 그 트리들끼리 '다수결 투표'를 진행하는 것이다.
각 트리는 독립적으로 학습되기에, 랜덤 포레스트 모델의 편향은 낮지만, 분산은 크다.
근데 그럼 문제가 있는데, 우리는 하나의 트레이닝 셋만 있는데 여기서 어떻게 다양한 모델을..? 내지..?
Bagging
데이터의 부트스트랩 샘플(재표본)을 사용해서 여러 트리를 학습시킬 수 있다.
최종 모델은 각 작은 모델의 평균 예측값이 된다.
근데 그렇다고 해서 모델의 분산을 줄이는 것에 그렇게 효율적인 것은 아니다.
강렬한 feature가 있다면.. 그게 항상 쓰일 것이기 때문이다.
그렇다면 여기서 아이디어로, 각 분할 과정에서, m feature 중 표본만을 사용하는 것이다.
m=sqrt(p)로 보통 쓰인다. p는 feature의 개수이다.
이런 방식으로 하면 개별 트리가 생겼을 때, 이는 제각각으로 과적합 됐을 것이다.
그래도 여기서 원하는 것은, 전체적인 모델은 낮은 분산을 갖는 것이다.
랜덤 포레스트 알고리즘
각 노드에서 임의로 m개의 특성을 선택한다.
가중치 엔트로피를 최소화하는 가장 좋은 특성인 x와 가장 좋은 나누는 값인 beta를 고른다.
예측하기 위해, T개의 결정트리에 물어보고 다수결 투표를 진행한다.
이 접근법을 위해선 T와 m이라는 파라미터가 필요하다.
휴리스틱으로 과적합 피하기
크기/깊이 제한,
불필요 가지 제거,
트리 앙상블로 과적합 완화
-> 최적이 아니라 경험적 방식임.
-> 대신, 누가 해봤을 때 이거 좋다고 밝혀지긴 함.
장점은,
분류/회귀 모두에 사용할 수 있고,
특징 스케일링이 필요하지 않으며,
중요 특성을 자동으로 식별할 수 있고,
비선형 관계를 처리해서 복잡한 특징 엔지니어링이 필요하지 않고,
과적합 가능성이 낮다.
위의 내용은 모두 트리의 '분류'에 대한 내용이었는데,
이제 회귀에 대해서도 똑같이 진행해보겠다.
선형 모델 대신 회귀 트리를 만드는 것이다.
트리 모델 in 회귀
단지 두 개의 수정만을 가지고, 우리는 dt 모델을 회귀에 사용할 수 있다.
1. 조건 나누기 : MSE로 측정된 모델의 예측 정확도를 향상시키기 위한 분할 기준을 선택하고자 한다.
- 분할할 예측 변수 j를 선택하고 새로운 영역의 가중 평균 MSE가 가장 최소가 되도록 분할할 t_j(임계값)을 고른다.
-> 원랜 엔트로피가 최소화되도록 분할했는데, 여기선 MSE를 줄이는 방향으로 분할한다.
<목적 함수>
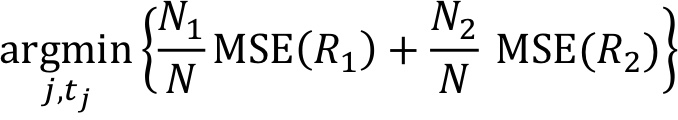
또는
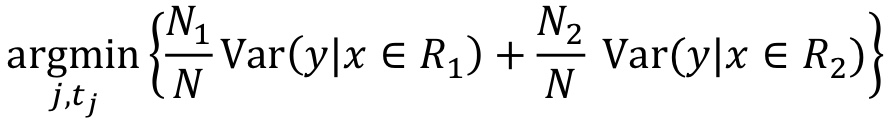
Ni는 Ri의 훈련 포인트 개수이고, N은 R의 포인트 개수이다.
분할 후, 두 영역에서의 평균 오차를 '최소화'하도록 분할값과 특성 선택하도록 함.
R에서 회귀분석을 위해 모델의 각 영역에 실수(해당영역 학습지점 출력값의 평균)를 라벨링하고자 함.
예를 들어,

이렇게 한 6.5 정도에서 기준선이 있고,
그 전후 데이터들의 평균값이 저 파란 선이 된다.
max_depth=1인 것은, node가 하나라는 것이고, 위 그래프에서는 x<6.5 인 node 하나만 있다고 생각하면 된다.

이 그래프에서는, max_depth=2라고 돼있는데, 그럼 node가 3개인 것이다.
루트노드는 x<6.5, 자식노드는 각각 x<3.5, x<7.4 정도의 내용일 것이다.
요런식으로 계속 진행하면.. 노드 수를 계속 증가시키면.. 다 쪼개서 평균을 구할 수 있을 것이다.
그럼 진짜 무슨 함수처럼 된다. 근데 그럼 당연히 과적합될 것이다.
여기서도 과적합을 방지하기 위해 조건들이 필요하다.
Stopping Conditions
최대 깊이 혹은 각 부분의 최소 포인트 개수에 도달한 경우,
순수 이득 대신, R 영역을 분할하는 정확도 이득을 계산할 수 있다.
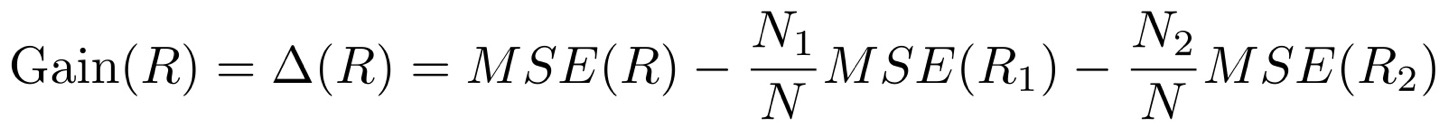
이 Gain은 에러가 얼마나 감소했는지에 대한 측도이고, 만약 gain이 특정 임계값보다 작다면 트리를 멈춘다.
그리고 MSE 대신 RSS(Residual sum of squares)를 사용할 수 있다.
결정트리는,
데이터를 선형으로 제한하지 않고, 분류 과정의 해석이 용이하다.
그렇지만 과적합 될 확률이 높고, 수학적으로 그다지 좋진 않다.
Boosting은 생략하겟어요~ㅎ
'AI > 데이터과학' 카테고리의 다른 글
| NN(Neural Networks), Convolution, Pooling (0) | 2024.12.14 |
|---|---|
| Vector Space Model, TFIDF, Word2vec (68-70p 추가) (2) | 2024.12.13 |
| 회귀/분류 (1) | 2024.12.10 |
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
| Association Rule Mining (0) | 2024.10.21 |
