본 포스팅은 충남대 김현 교수님의 강의자료를 바탕으로 작성한 글입니다.
몬테카를로 방법이란,
무작위 샘플링을 바탕으로 반복 샘플링을 통해 값을 근사하는 방법이다!
ex) 사각형 안에 원 그린 후, 무작위 점 찍어서 점 개수로 원 넓이 추정
그럼 이게 강화학습에선 어떻게 쓰이냐 하면,
환경에 대한 dynamics를 사전에 알 수 없다는 전제 하에, agent가 환경과 상호작용 통해 s, a, r, s'를 얻고, 가치함수를 추측하는 데 사용
에피소드를 반복해 나가면서 각 state의 보상의 합인 state-value function이 누적되고, 이 평균으로 실제 값을 추정
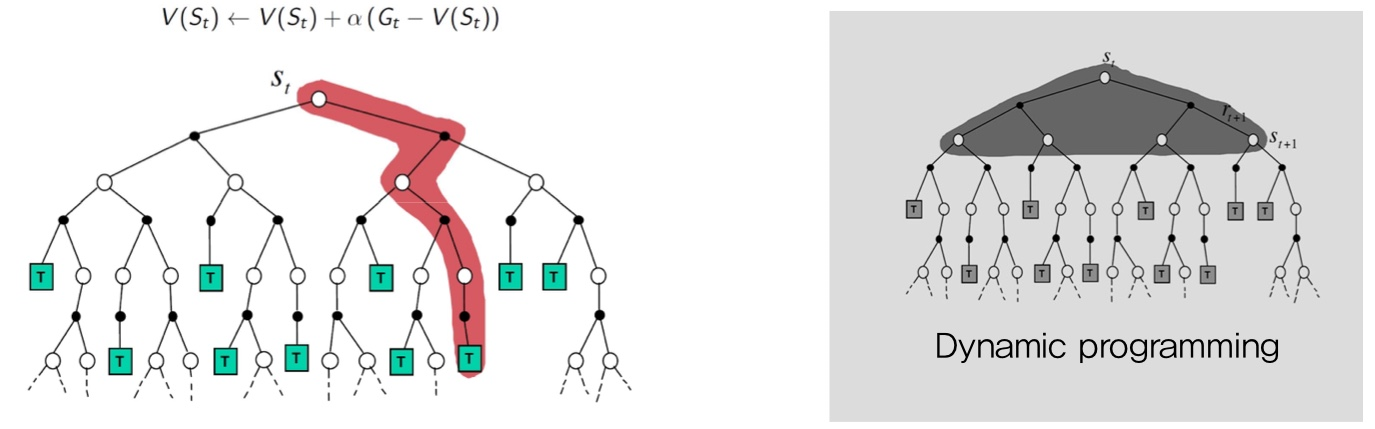
DP는 단계씩 나아갔지만,
MC는 우선 끝까지 간다!!
Goal : policy가 주어졌을 때, 이 policy로 만들어지는 episodes로부터 value function 구하는 문제
Return : 한 episode 끝날 때 받는 모든 Reward 합

여기서, 임의 state의 value function은 expected return 대신 empirical mean return이용
ex) MC Prediction 계산시, G0 = R1+rG1, G1 = R2+rG2.. 이런식으로 맨 마지막 Gt만 알면 G0까지 계산 가능
First visit VS. Every visit
first visit : 아예 완전히 끝나면 계산
every visit : state s에 도달할 때마다 s에 대한 reward 계산
Incremental Mean이란?
Return의 평균 구할 때 점진적 방법 이용하는 것.


DP는 model-based, RL은 model free..
RL에선 정책 개선 위해 v대신 q이용
Control 문제 위해서 Exploration을 반드시 고려해야 하는데,
왜냐면 맨날 q를 최대화할 때 정책 개선이 되는데, 그때 선택받지 않는 a들에 대한 value가 계산되지 않기 때문.
그래서 더 좋은 정책을 못 찾는 경우도 있음
따라서.. 이런 문제를 해결하기 위해 3개의 방법이 있음.
1. Exploring Starts
episode의 시작점을 바꾸는 건데, 현실적으로 어려움
2. Stochastic Policy
가장 일반적으로 e-greedy policy가 있고, e의 확률로 랜덤 a를 택하는 것임.
e-soft policy는 모든 a에 대해 최소한 e의 확률을 부여해서 탐험할 수 있도록.(e-greedy는 e-soft에 포함됨) 그리고 이 e-soft는 exploring start가 필요없음!
3. Off-policy Learning
on-policy vs. off-policy
on policy learning : 현재 정책에 따라 액션 선택 후 그 결과로 정책 업뎃
off policy learning : 액션 선택 위한 정책과, 실제 평가와 개선 위한 정책이 별도로 있는 학습 방법.(DQN)
-> behavior policy는 action 선택 후 환경 상호작용 결과 생성, target policy는 behavior policy의 결과로 더 좋은 정책 찾음
-> but, behavior policy에서 수집된 데이터를 바로 target에 적용할 수가 없기에, Importance Sampling 사용
* Importance Sampling 이란?
어떤 확률분포에서 기댓값을 계산하고 싶은데 데이터 샘플링이 어려울 때, 샘플링이 쉬운 다른 확률분포를 이용해서 기댓값 추정
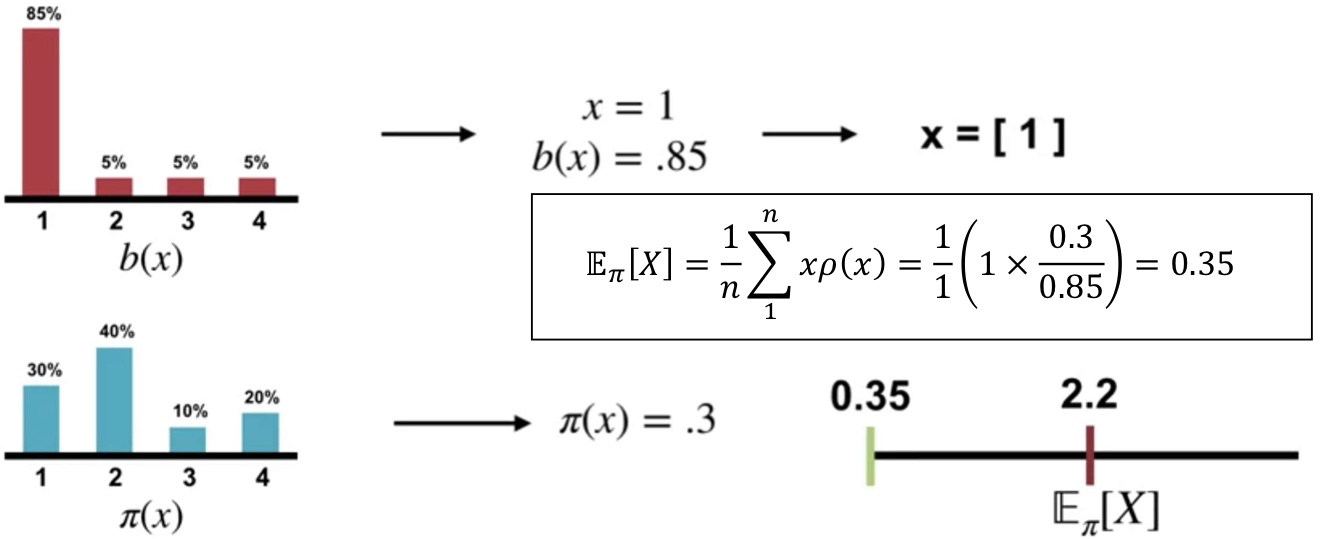
위의 그래프 분포에서 샘플링해서 밑의 pi 분포를 추정하는..
저 공식으로 계속 n 증가시키면서 계산하면 언젠가 수렴함
MC 학습의 특징!
- Model-Free! MDP 모델을 알 필요가 없다!
- 샘플링 기반 시도 후 다음 상태와 그때의 보상 확인
- 각 state의 상태가치함수가 다른 state의 가치함수와 독립적 계산 (DP에선 연관됐었음)
- 각 state의 value를 추정할 때 필요한 계산이 MDP 모델 크기와 무관
- 종료 상태가 있어야만 적용 가능. 충분한 탐색이 보장돼야 함.
'AI > 강화학습' 카테고리의 다른 글
| 시간차 학습(Temporal Difference Learning) (0) | 2024.10.24 |
|---|---|
| Dynamic Programming in RL (2) | 2024.10.23 |
| Value function & Bellman equation (0) | 2024.10.17 |
| Markov Decision Process (8) | 2024.10.16 |
