본 포스팅은 충남대 김현 교수님의 강의자료를 바탕으로 쓴 글입니다.
Dynamic Programming이 어떤 것인지 한 번쯤은 들어봤을 것이다.
가장 많은 예시로 쓰이는 건 피보나치 수열이다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55... 이렇게 앞의 두 숫자가 더해져서 뒤의 숫자를 만드는데,
그럼 10번째 피보나치 수를 구하려면 앞의 9개 숫자를 다 구해야 하면.. 너무 오래 걸릴 것이다.
그래서 이 결과를 저장해두고 두고두고 쓰는 것이다.
이걸 강화학습에 적용하면, 두 단계로 나뉜다.
정책 평가와 정책 개선으로!
1. 정책 평가 (Prediction)
모델에 policy가 주어질 때 policy를 평가하는 단계.
S, A, P, R, gamma와 policy가 주어지면 value function을 내놓는다.
근데 어떻게..?
이전 글에서 나온 Bellman expectation equation을 반복적으로 적용하면 된다.
각 iteration에서 모든 s에 대해 v_k(s')의 값으로 v_(k+1)(s)를 업뎃 시킬 수 있다.
식도 진짜 Bellman expectaion equation과 똑같다.

하나도 다를 게 없다..
그냥 저 update rule 을 기반으로 상태가치 추정치를 반복 업뎃하면 그게 반복적 정책평가 이다.
그러다가.. 저 V_(k+1)이 상태가치 추정치인데,
모든 상태에서 V_(k+1)이 V_k, 즉 추정치가 변하지 않는다면?
V_k가 Bellman equation의 유일해가 돼버린다.
근데 이게 DP랑 뭔 상관? 이냐 하면,
우선 모든 state에 대해 각각 2개의 배열 (V-current value function, V'-updated value function)을 할당한다.
그러고 각 state별로 한 step씩 진행하면서 value를 update한다.

요런 식으로.. V_k를 미리 다 구해놓고 이걸 식을 적용해서 V_(k+1)에다 넣음

요로케.. V를 가지고 V'를 다 구해준다.
그 담에, V_(k+1)값을 아예 복사해서 V_k에 넣어준다. 이게 업뎃!
자! 실제 예시를 봐보자!

지금 이 문제를 할 거다.
저 검정 부분은 그냥 고려하지 않는 부분인 거 같다.
사실 검정 부분을 잘 모르겠다.. 그냥 여길 생각하지 않고 해보자
모든 곳의 V를 우선 0으로 초기화해준다. 그리고 똑같은 격자를 하나 더 만들어서 V'의 값을 저장할 것이다.
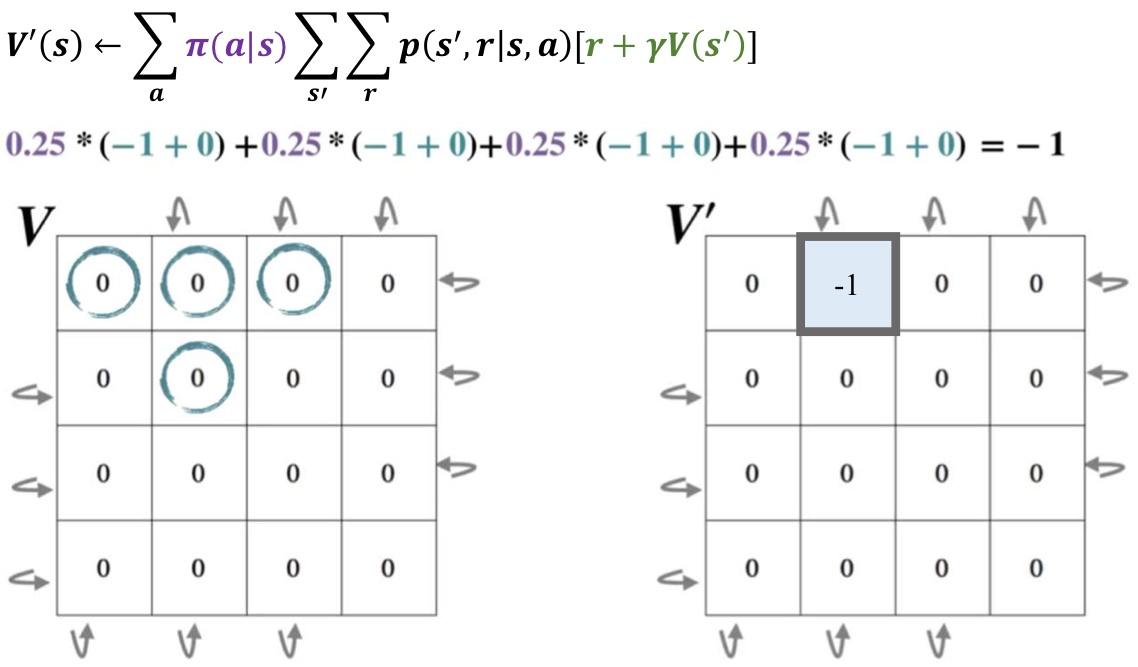
이렇게, V를 보고 V'의 모든 부분을 채워줄 것이다!
V'의 1행 2열 값이 변했다고 그 주변 V'이 영향을 받진 않는다.
그냥 오로지 V만 보고 V'의 값을 계산해나간다!
그럼 아래와 같이 V'이 변하고, 그 값을 다시 V에 복사시켜 주면 된다!

이렇게 V'의 값을 V에 붙여넣어주고, V'는 다시 초기화시킨다!
뭐 초기화 시켜주지 않아도 된다. 어차피 값들이 업뎃 될 것이니
그럼 저 변화한 V를 보고 다음 V'를 또 계산한다.

이렇게! 또 V'를 계산하게 됐고,
그럼 이제? 저 값을 다시 V에 붙여넣기 하면 된다!
이 과정을 쭉쭉 반복하면 된다.
그러다가 어느 순간 엡실론이 threshold보다 작아지는데,
그럼 그걸 수렴한 것이라고 생각하면 된다.
마지막으로, 그걸 수도코드로 나타내면 이렇게 된다!

2. 정책 개선 (Control)
주어진 policy를 더 나은 policy로 개선하는 단계.
S, A, P, R, gamma가 주어지면 optimal value function과 optimal policy를 내놓는다.
전에 optimal policy 찾았던 것처럼 그냥 greddy action을 찾는 과정을 반복하묜 된다.
아까 위에서 V를 계속 변경하다가 어느 순간 수렴했을 때의 V를 생각해보자. (policy는 uniform)
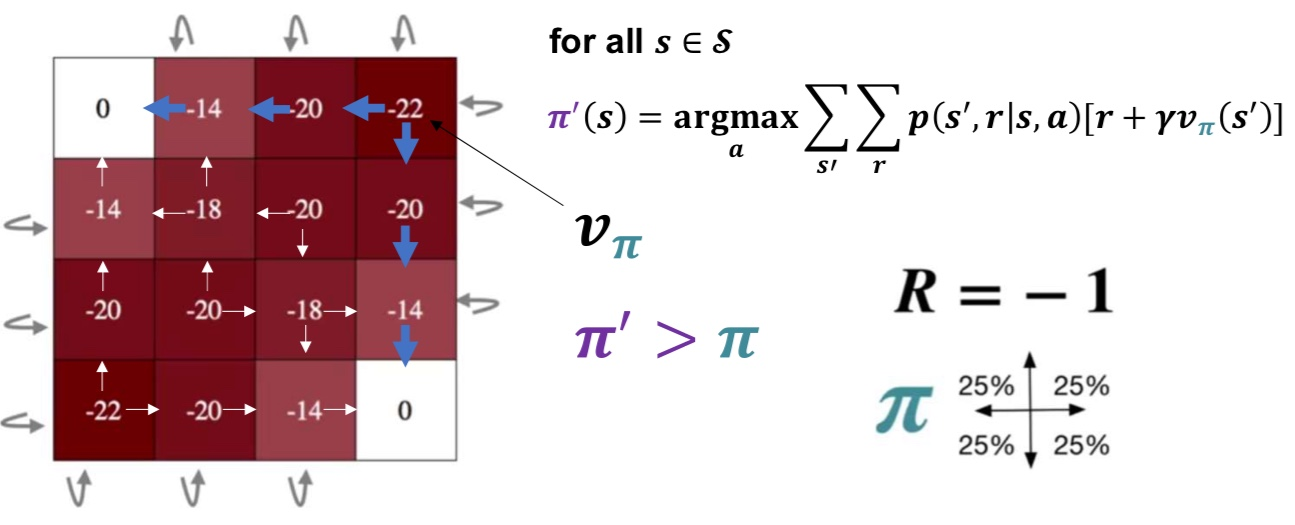
요건데,
policy 보면 자기 주변 셀 중 가장 큰 값들로만 이동한다는 것을 알 수 있다!
밑의 사진은, 정책 평가를 k번씩 한 후 control 한 결과물이다.

3. 정책반복 알고리즘
우리가 위에 배운 정책평가와 정책개선을 묶어서 최적의 정책을 이끌어내는 것을 정책반복이라고 한다.
요기선 p()가 더 큰 지점을 찾는 거라, sigma(pi(a|s))를 고려하지 않는다!
정책 평가와 정책 개선을 수도코드로 본다면,

이렇게 생각할 수 있다.
정책 평가는 V가 수렴할 때까지,
정책 개선은 가장 큰 V를 만나는 action을 policy로
그냥 이 두 개를 묶은 게 정책 반복 알고리즘,
Policy Iteration Algorithm이다.
이건 현재 정책을 평가하고 개선하는 방식으로 작동.
정책 평가에서 상태 가치를 반복 계산하고, 정책 개선으로 갱신
우선 random policy로 iterative policy 평가를 수행(반복)
그러면 개선된 policy를 딱 정할 수 있음. 그 state에 대해.
그담에 모든 state에 대해 iterative policy 평가를 수행하는데, 이땐 random policy가 아니라 위에서 나온 개선된 policy임.
그러면 policy가 또 개선될 거임.
그럼 전의 policy와 개선된 policy를 비교함
그담에 또 이걸 현재의 policy로 설정하고.. 또 iterative policy 평가를 하고.. 이러다보면 이제 결과 policy의 변화가 안 생기는 지점이 나올 것임.

막 요런 식으로 평가하고 policy 업뎃하고 이 과정을 계속 반복하는 것임 수렴될 때까지.
그래서 시간이 좀 오래 걸린다는 단점이 있음.
4. 가치 반복 알고리즘
이건 각 상태에서 가치 함수 갱신하면서 optimal value function찾음.
즉, 정책 평가랑 개선을 한 번에 수행함.
정책 반복 알고리즘에 비해 반복적으로 정책 평가하는 과정을 생략하면서 더 빠르게 수렴 가능하다.
정책 반복은 벨만 기대 방정식 사용, 가치 반복은 벨만 최적 방정식 사용!
정책반복은 모든 state를 한 번 본 담에 policy 업뎃, 가치반복은 한 번 시도마다 업뎃

요게 둘이 다른 점!
왼쪽은 정책반복,
오른쪽은 가치반복
DP는 MDP 모델 정보를 모두 알아야 하고, 각 state에서 다름 상태에 대한 value function을 업뎃해야 하기에 state가 늘어날 수록 계산량이 급격히 많아진다.
표로 정리!

'AI > 강화학습' 카테고리의 다른 글
| 시간차 학습(Temporal Difference Learning) (1) | 2024.10.24 |
|---|---|
| Monte Carlo Learning in RL (0) | 2024.10.24 |
| Value function & Bellman equation (0) | 2024.10.17 |
| Markov Decision Process (8) | 2024.10.16 |
