본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
Box and whisker plot
양적 변수에 대한 그래프!
First or lower quartile은 25%, Second quartile은 50%, Third or Upper quartile은 75%
따라서 First & Third quartile은 항상 middle 50%의 데이터를 포함하고 있다.
데이터 분포를 볼 때 자주 쓰이는 box plot의 IQR은, Q3-Q1로 계산된다.
여기서 Whiskers는 이상치 기준선을 나타내는데, Q1-1.5*IQR 부분과 Q3+1.5*IQR 부분을 말한다.
이 Whisker를 넘어가는 부분을 이상치로 정한다.
Histogram
Rug plot을 아는가? 이는 1차원 데이터를 쭉 나열한 그래프라고 보면 된다.
x축은 데이터의 범위이고, 데이터가 있는 곳마다 그래프가 그려져있다.
따라서 데이터가 한 곳에 몰려서 찍혀있을 수도 있다.
그리고 그 높이는 모든 데이터가 다 같다. 그냥 어디에 몰려있는지 정도 확인할 수 있다.
이러한 Rug plot을 좀 스무스하게 그린 버전이 Histogram이다.
히스토그램은 어디에 데이터가 얼마나 있는지 볼 수 있다. 각 데이터의 빈도에 따라 높이가 다르기 때문이다.
KDE
Kernel Density Estimation은 데이터셋으로부터 확률 밀도 함수를 추정할 때 쓰인다.
조금 어렵게 느껴질 수도 있지만, 간단히 생각하면 된다!
일단 커널을 만든다. 어떤 확률분포라고 생각하면 되고, 따라서 커널과 x축 사이 공간의 넓이는 1이다.
그래서 이 커널을, 우리가 뽑은 샘플 데이터 모든 위치에 놓는다.
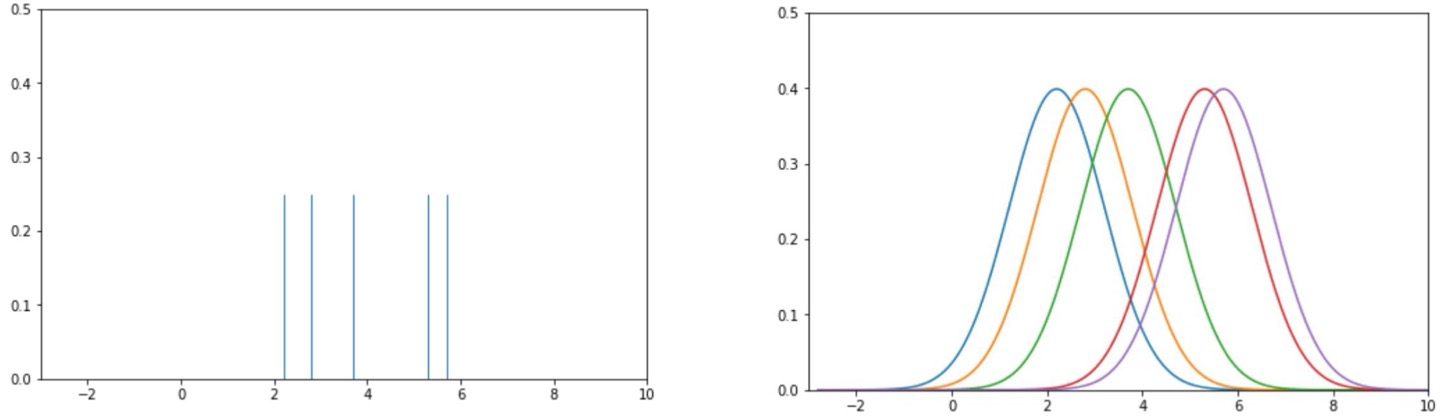
즉, 커널이 이렇게 양옆으로 쭉 늘어설 것이다. 당연히 겹치는 부분도 생길 것이다.
그럼 이제 우리가 원하는 것은, 이걸 하나의 분포로 다시 만드는 것이다.
근데.. 지금은 넓이가 1인 커널이 데이터 수 n만큼 쌓여있으니까 총 넓이가 n일 것이다.(겹친 것은 생각하지 않고, 커널의 크기만 따지면)
근데 확률 분포가 되려면 총 넓이가 1이 돼야 하므로, 모든 커널의 값들을 다 n으로 나눈다.
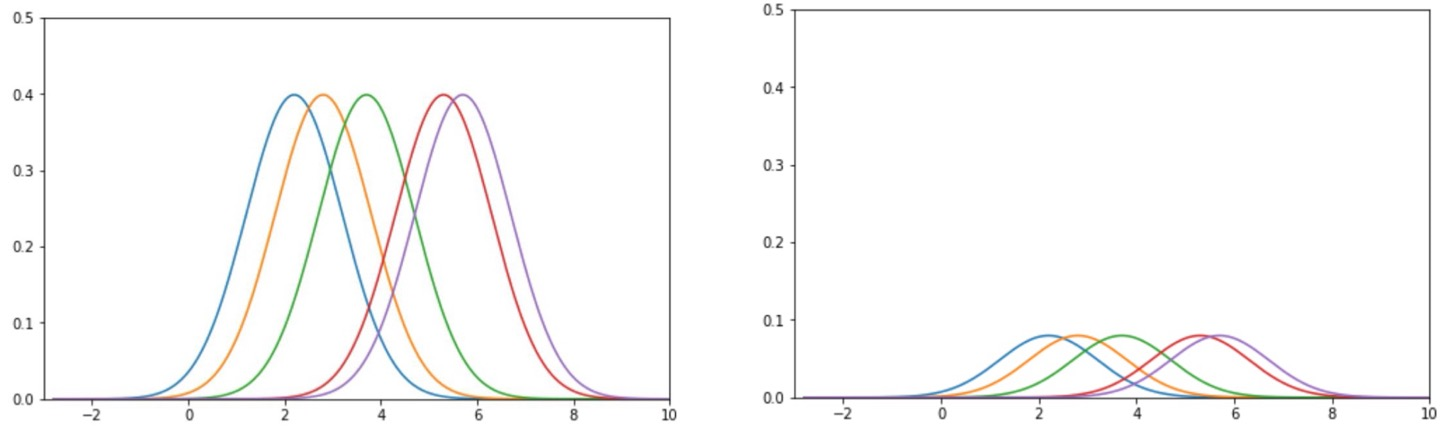
그 후, 겹치는 부분은 그 커널의 값들을 다 더해서 수직으로 쌓는다.
그럼 넓이가 1인 확률 분포처럼 생긴 그래프를 만들 수 있을 것이다.
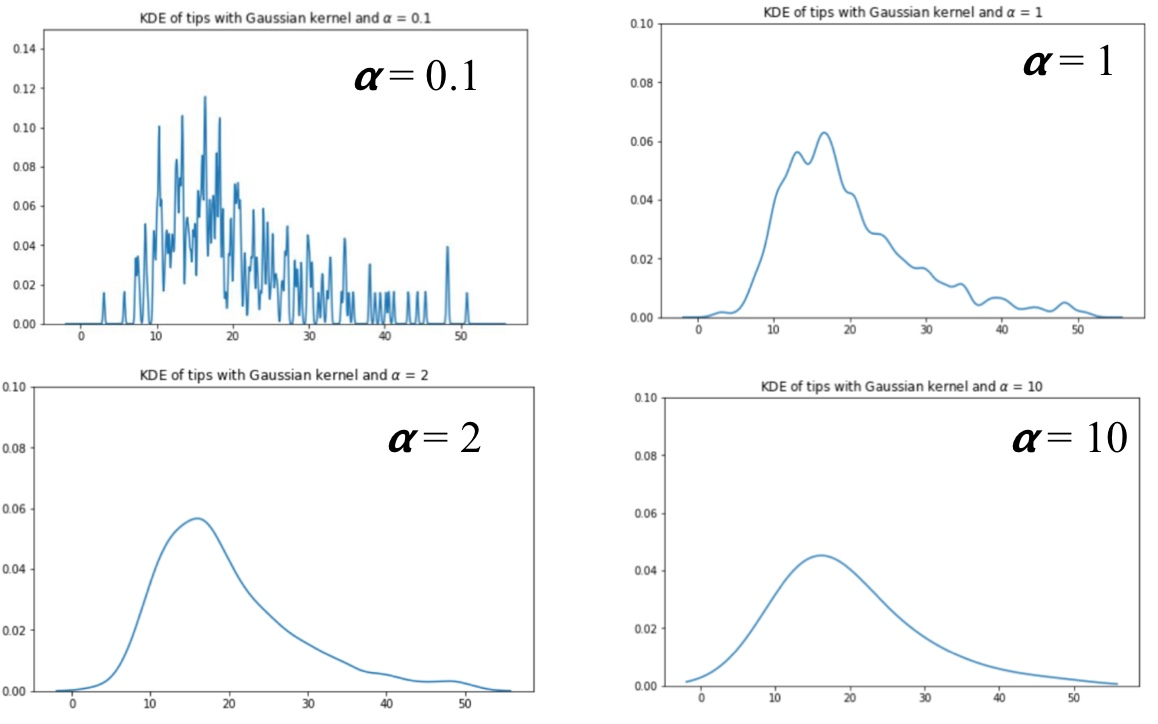
따라서 이건 커널이 어떻게 생겼는지가 중요할 것인데, bandwidth라는 alpha값이 이를 결정한다.
그럼 이 alpha값이 달라짐에 따라 뭐가 달라지냐면, 알파가 커질 수록 그래프는 스무스해지지만, 따라서 정보가 손실된다.
그리고 이 알파는 정규분포에서 분산을 의미한다.
'AI > 데이터과학' 카테고리의 다른 글
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
|---|---|
| Association Rule Mining (0) | 2024.10.21 |
| 상관관계 분석과 가설 검정 (0) | 2024.10.21 |
| EDA의 일부, 데이터 전처리와 특성 추출 (2) | 2024.10.19 |
| 정규표현식 (Regular Expression) (0) | 2024.10.19 |
본 포스팅은 충남대 이종률 교수님의 강의자료를 바탕으로 작성한 글입니다.
Box and whisker plot
양적 변수에 대한 그래프!
First or lower quartile은 25%, Second quartile은 50%, Third or Upper quartile은 75%
따라서 First & Third quartile은 항상 middle 50%의 데이터를 포함하고 있다.
데이터 분포를 볼 때 자주 쓰이는 box plot의 IQR은, Q3-Q1로 계산된다.
여기서 Whiskers는 이상치 기준선을 나타내는데, Q1-1.5*IQR 부분과 Q3+1.5*IQR 부분을 말한다.
이 Whisker를 넘어가는 부분을 이상치로 정한다.
Histogram
Rug plot을 아는가? 이는 1차원 데이터를 쭉 나열한 그래프라고 보면 된다.
x축은 데이터의 범위이고, 데이터가 있는 곳마다 그래프가 그려져있다.
따라서 데이터가 한 곳에 몰려서 찍혀있을 수도 있다.
그리고 그 높이는 모든 데이터가 다 같다. 그냥 어디에 몰려있는지 정도 확인할 수 있다.
이러한 Rug plot을 좀 스무스하게 그린 버전이 Histogram이다.
히스토그램은 어디에 데이터가 얼마나 있는지 볼 수 있다. 각 데이터의 빈도에 따라 높이가 다르기 때문이다.
KDE
Kernel Density Estimation은 데이터셋으로부터 확률 밀도 함수를 추정할 때 쓰인다.
조금 어렵게 느껴질 수도 있지만, 간단히 생각하면 된다!
일단 커널을 만든다. 어떤 확률분포라고 생각하면 되고, 따라서 커널과 x축 사이 공간의 넓이는 1이다.
그래서 이 커널을, 우리가 뽑은 샘플 데이터 모든 위치에 놓는다.

즉, 커널이 이렇게 양옆으로 쭉 늘어설 것이다. 당연히 겹치는 부분도 생길 것이다.
그럼 이제 우리가 원하는 것은, 이걸 하나의 분포로 다시 만드는 것이다.
근데.. 지금은 넓이가 1인 커널이 데이터 수 n만큼 쌓여있으니까 총 넓이가 n일 것이다.(겹친 것은 생각하지 않고, 커널의 크기만 따지면)
근데 확률 분포가 되려면 총 넓이가 1이 돼야 하므로, 모든 커널의 값들을 다 n으로 나눈다.

그 후, 겹치는 부분은 그 커널의 값들을 다 더해서 수직으로 쌓는다.
그럼 넓이가 1인 확률 분포처럼 생긴 그래프를 만들 수 있을 것이다.
따라서 이건 커널이 어떻게 생겼는지가 중요할 것인데, bandwidth라는 alpha값이 이를 결정한다.
그럼 이 alpha값이 달라짐에 따라 뭐가 달라지냐면, 알파가 커질 수록 그래프는 스무스해지지만, 따라서 정보가 손실된다.
그리고 이 알파는 정규분포에서 분산을 의미한다.

'AI > 데이터과학' 카테고리의 다른 글
| 분류(K-Means, Agglomerative Clustering, DBSCAN) (3) | 2024.10.21 |
|---|---|
| Association Rule Mining (0) | 2024.10.21 |
| 상관관계 분석과 가설 검정 (0) | 2024.10.21 |
| EDA의 일부, 데이터 전처리와 특성 추출 (2) | 2024.10.19 |
| 정규표현식 (Regular Expression) (0) | 2024.10.19 |
