윤곽선 추출해내기!
윤곽선이 머냐? pixel을 봤을 때, 날카롭게 각진 애들이다.
이걸 어떻게 찾아내지?
이미지의 픽셀값을 그래프로 나타냈을 때, 값이 급격히 변하는 부분이 있다. 근데 이걸 정확히 구하려면?
한 번 미분하면, 그 변하는 구간에서 극값이 발생함. 이거로 윤곽선 찾기 가능.
근데.. 이 이미지를 어떻게 미분할 것이냐.. 그건 너무 복잡하잖아
잘 생각해보면, 미분은 어떤 식이냐면,
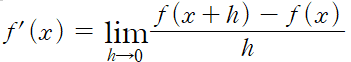
원랜 이런 식임. 근데 얠 좀만 더 변형해보면,

이렇게 쓰기도 함. 그렇담 이 식에서, 만약 h에 2를 넣는다면?

이렇게 됩니당. 근데 이걸 벡터의 곱으로 표현할 수 있단 사실..
어떻게냐면, 이제 x, x-1, x+1값이 있음. 그럼 이 좌표들의 값은 각각 f(x), f(x-1), f(x+1)일 것임.
순서대로 쓰면, f(x-1), f(x), f(x+1) 이 됨.
여기에다가.. 만약 (-1, 0, 1) 필터를 곱한다면?!
f(x+1)-f(x-1)이 된다는 점. 그럼 미분값이랑 똑같음. 물론 미분결과는 2로 나눠져있지만.. 그건 극값 구할 때는 별 상관 없음.
그래서 사실 극값을 구하는 것이기 때문에 필터가 (1, 0, -1)이어도 상관없긴 함.
그럼 결국, (1, 0, -1)필터로 필터링 진행하면 경계선 구할 수 있다는 건데,
이 필터만 쓰면, noise에 너무 취약함.. 그래서
노이즈를 제거하고 이 필터를 쓰면 좋은데,
애초에 노이즈제거+극값 필터를 더해주면 되니깐, 그걸 섞은 필터가 sobel filter이다.
(1, 0, -1) (1 (1, 0, -1)
(2, 0, -2) = 2 *
(1, 0, -2) 1)
이렇게 생긴 필터이다. blurring filter * 1D derivative filter인 것~
이건 근데.. 저렇게 생기면.. vertical filter임.
저걸 transpose하면 horizontal filter임.
이렇게 구한 값을 image gradient라고 하고, 그 각 x좌표 미분값의 제곱과 y좌표 미분값의 제곱을 더해서 루트씌운 값이 magnitude인데, 이 값은 edge 가 더 강해진 것이다.
근데 소벨필터로는 blurring이 얼마 되진 않으니까, gaussian filter 등으로 잡음 대처 후 sobel filter를 하면 좋다.
근데.. 그럼 그냥 차라리, 소벨필터가 blur filter * derivative filter인데, 그냥 gaussian filter * derivative filter를 하는 건 어때?
그렇게 해서 만들어진 것이 DoG gilter.
가우시안을 미분해서 이걸 필터로 쓰는 것임^^
이것도 x, y에 따라 생김새가 다름.

앞에가 x에 대한 필터, 뒤에가 y에 대한 필터
근데 이젠.. 이렇게 한 번 미분한 필터 말고 두 번 미분한 필터를 사용할 수도 있음.
한 번 미분한 필터는, 극값을 가지는 좌표를 찾는 것이 목표였지만,
두 번 미분한 필터는, zero-crossing point라고, 부호가 바뀌는 지점을 찾는 것이 목표이다.
그럼 이제.. 아까 그 미분식을 또 미분해서 생기는 식을 써보면,

이 식이 된다.
if h = 1, filter = (1, -2, 1)
if h = 2, filter = (1, 0, -2, 0, 1)
...
이러한 필터를 Laplace filter라 한다.
이미지를 Laplace 하려면, 이러한 필터를 쓰면 된다.
(0, 1, 0)
(1, -4, 1)
(0, 1, 0)
이 필터를 약간씩 바꾼다면.. 부호를 변경할 수도 있고, 아니면 꼭짓점 값들을 0에서 1로 다들 바꿔주고, 그럼 4가 더해졌으므로 중앙값에서 4를 빼줘서 총합을 1로 맞춰주는 방법이 있다.
이러한 Laplace 과정에서도, 노이즈를 없애는 선행과정은 반드시 필요하기 때문에, 가우시안 필터를 써줄 건데,
DoG 필터처럼 가우시안을 두 번 미분한 필터를 사용한 것과 같다.
근데 이제 결과적으로 LoG와 DoG의 차이점은, LoG는 zero-crossing한 결과이기 때문에, 윤곽선이 두 줄로 나타난다.
DoG는 그냥 한 줄로 나타난다.
그래서 이제.. 진짜 마지막으로 우리가 원하는 건, 애매한 윤곽선이 아니라 진짜 윤곽선, 딱 선만 그어진 그런 그림을 원한다. 그렇다고 그 윤곽선이 그리 두껍지도 않은.
그 과정은, 스무딩하고, 미분값을 구하고, nms로 엣지를 특정화함.
X-Derivative of Gaussian의 제곱과, Y-Derivative of Gaussian의 제곱을 더해서 루트를 씌우면, 그게 gradient magnitude
nms의 목적은?
윤곽선을 얇게 하기!
그럼 magnitude값이 클수록 edge일 확률이 높은 것.
그 과정은?
접선에 직교한 선을 그어서 그 중 max값만 골라서 걔로 윤곽선 만들 거임.
예를 들어, 3*3으로 본다 하면, 중앙값인 q에서 기울기를 찾아 3*3 필터의 벽에 닿는 점 두 개의 값과 q의 값을 비교해서 max값을 업뎃시킨다.
double thresholding은,
이제 T_Low, T_high를 정해서,
만약 T_high보다 큰 값이라면 무조건 edge!! -> strong edge
만약 T_Low보다 작은 값이라면 무조건 edge 아님.
나머지 값들은 weak edge!
그럼 이제, Hysteresis thresholding을 하면,
만약 weak edge를 쭉 이었을 때 strong edge랑 연결된다면 edge로 판별하고, 만약 weak끼리만 있다면 edge가 아니라고 볼 수 있다.
시그마 값은 클수록 smoothing이 잘 되므로, edge가 줄어든다.
이런 edge 정하는 문제는 정답이 있는 게 아님..
무늬까지 하든 경계선만 하든.. 머 상관없음 내 목표까지 하면댐.
'AI > 컴퓨터비전' 카테고리의 다른 글
| Segmentation (1) | 2024.06.16 |
|---|---|
| Morphological (0) | 2024.06.15 |
| image resizing (0) | 2024.06.15 |
| Image filtering (0) | 2024.06.15 |
| Image 기초 (0) | 2024.06.15 |
