본 포스팅은 <R을 활용한 선형회귀분석> 책을 바탕으로 작성한 글입니다.
회귀분석을 하고, 그 자료에 대한 진단 방법으로 여러가지가 있는데,
이 글에서는 우선 "영향력 관측치"에 대해 알아보려 한다.
영향력 관측치
최소제곱법을 통해 beta_hat과 s^2를 구했을 때, 이 값들은 하나 혹은 소수의 관측치에 의해 큰 영향을 받는 경우가 있다.
저렇게 큰 영향을 주는 관측치(들)를 영향력 관측치라고 한다.
그럼 이 영향력 관측치를 어떻게 찾냐 하면은, '영향력 측도'를 이용하면 된다.
이는 영향력을 수치화하는 측도이고, 보통 이는 잔차와 지렛값의 증가함수로 나타내진다.
그럼 잔차와 지렛값을 알아보겠다.
잔차
잔차는 관측값과 적합값의 차이이다. 즉, Y-Y_hat이다.
이 잔차는 e로 나타내지고, 이는 오차(엡실론)의 추정치이다.
오차와 잔차의 차이점은, 오차는 모집단에서 회귀식에 대한 편차값이고 잔차는 표본집단에서 회귀식에 대한 편차값이다.
따라서 오차의 분포 및 등분산성에 대한 가정을 잔차를 이용해 검토한다.
그런데, 여기서 오차항의 독립성을 가정하고 잔차를 구하면 이 잔차는 서로 상관관계를 가지게 된다.(독립 X)
모자행렬 H를 이용하면 잔차벡터는 (I-H)y로 나타낼 수 있다.
따라서 잔차벡터의 기댓값벡터는 0이고, 분산-공분산행렬은 (I-H)sigma^2이다.
그럼 여기서 ei의 분산은 분산-공분산행렬의 i번째 대각원소로, (1-hii)sigma^2 이다.
그리고 ei와 ej의 공분산은 비대각원소로, (0-hij)*sigma^2 이다.
이걸 보면 잔차들은 오차들과 달리 같은 분산을 가지고 있지 않다는 것을 알 수 있다. (등분산성 성립 X)
그럼 이런 잔차를 가지고 오차의 가정의 타당성을 조사하는 것이 맞을까? 싶지만,
잔차는 관측할 수 없는 값인 오차에 가장 근접한 값이고, 대부분 hij는 0에 가깝기에 큰 문제는 아니다.
그리고 이 잔차는 척도무관하지 않기에 단위가 없는 값으로 변화시키려 한다.
단위가 없는 값으로 표현하면 내 표준화잔차와 외 표준화잔차로 나눌 수 있다.
내 표준화잔차
보통 표준화하는 식을 이용해서, ei에서 평균인 0을 빼고 표준편차인 sigma*sqrt(1-hii)로 생각할 수 있고,
여기서 sigma가 미지이기에 비편향추정량인 s를 대신 사용해서 표준화시키면 이를 ri, 내 표준화잔차라 한다.
내 표준화잔차의 절댓값이 큰 경우를 특이점(outlier)이라고 한다.
근데 얼마가 되면 크냐? 를 보기 위해 기준값이 필요한데, 이 ri는 표준정규분포를 따르진 않지만 편의상 이를 사용해 근사적으로 2를 기준값으로 보고 있다.(정규분포에서 임계값으로 주로 사용되는 1.96의 근사값인듯 하다.)
외 표준화잔차
근데 이제 내 표준화잔차는 관측치가 분자의 ei와 분모의 s를 계산할 때 동시에 사용되는데, 그래서 특이값이 많이 표시나진 않는다.
그래서 ei와 독립적으로 계산되는 sigma의 추정치가 필요한데, 그걸 이제 만들어보겠다.
현재 사용되는 관측치와 독립적인 다른 자료가 있는 경우 이걸 이용하면 되겠지만, 보통 그런 자료가 없으므로~
지금 사용되는 i번째 관측치 Yi를 제외시키고 n-1개의 관측치로 회귀모형을 적합시켰을 때 나오는 분산의 비편향추정값을 쓰는 것!
i번째 관측치를 제외한 분산추정값을 s(i)^2라 하면, ei의 표준화로 ei/s(i)*sqrt(1-hii)를 쓸 수 있다.
이걸 ri*라 하고, 외 표준화잔차 라고 부른다.
그리고 이 ri*는 자유도 n-p-1인 t분포를 따른다는 장점이 있다. 따라서 자유도가 충분히 크다면 ri*의 절댓값이 2보다 크면 이상치!
근데 그 s(i)^2를 그럼 n개의 식을 다시.. 적합시켜야 하나? 그건 아니다. 원래의 s^2에서 구할 수 있다.
s(i)^2 = s^2 * (n-p-ri^2) / (n-p-1) 로 구할 수 있다.
그리고 이를 다시 써보면 ri*와 ri의 관계는
ri* = ri * sqrt((n-p-1)/(n-p-ri^2))로 볼 수 있다.
지렛값
아까 말했던 영향력 측도를 계산할 때 필요한 것이다. 사실 잔차 얘기할 때도 이 지렛값이 나왔다.
모자행렬 H의 i번째 대각원소인 hii, 즉, xi'(X'X)^(-1)xi를 말한다.
반응변수인 Y가 식에 하나도 안 들어있는 걸로 봐선, 설명변수에 의해서만 결정된다는 것을 알 수 있다.
이 지렛값은 i번째 관측치 xi가 중심 x_bar에서 떨어져 있는 정도를 나타낸다.
이 거리는 유클리드 거리가 아니라 설명변수간 상관관계가 감안된 통계학적인 거리, 마할라노비스거리이다.
마할라노비스는 타원 혹은 타원구를 나타내는 공식이다. 지렛값이 같은 관측치들은 타원 혹은 타원구를 형성한다.
이 마할라노비스 거리 밖의 점들은 상대적으로 높은 지렛점이라고 할 수 있다.
즉 x_bar 근처 관측치의 지렛값은 작고, x_bar에서 멀리 떨어져 있다면 지렛값이 크다.
이 hii를 다시 나타내면,

뒤 항 때문에 당연히 xi와 x_bar가 차이날수록 hii가 커진다.
지렛값의 특징 - 설명변수가 p-1개인 중선형회귀모형에서
1) 모든 hii를 더하면 p(행렬 X의 열의 개수)이다.
2) hii는 1/n보다 크거나 같고 1보다 작거나 같다. (식을 보면 당연함)
3) hij제곱은 항상 hii*hjj보다 작거나 같다.
지렛값의 값이 큰 관측치를 높은 지렛점이라고 한다.
그리고 i번째 적합값 yi_hat에 대해서 다음 식이 성립한다.
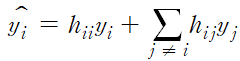
위의 지렛값의 특징에서 봤듯이, 보통 대각원소 hii가 비대각원소 hij보다 크기에 yi_hat에 미치는 영향이 가장 큰 반응변수는 yi이다.
그리고 만약 hii도 큰 값이라면 yi_hat은 주로 yi에 의해 결정돼진다.
따라서 hii값이 yi의 영향력을 판단하는 중요한 도구가 된다.
근데 당연히, 잔차분산을 생각해보면 hii가 1에 가까워지면 잔차분산이 0에 가까워지므로 yi_hat이 yi와 흡사해진다는 것도 알 수 있다.
즉, hii가 클수록 yi는 회귀식에 더욱 영향을 많이 끼친다.
그럼 이제 지렛값이 크다 라고 할 수 있는 기준점을 찾아야 하는데,
이 지렛값은 오직 설명변수 X에 의해서만 결정되므로 X가 중요한데,
보통 기준치는 hii의 평균인 p/n에 2를 곱한 2p/n를 사용한다.
그럼 이제 진짜 목표였던 영향력 관측치에 대해 다시 알아보겠다.
영향력 관측치
아까 위에서 말했듯, 어떤 관측치가 추정량 beta_hat또는 표본분산에 큰 영향을 미칠 때 이를 영향력 관측치라 한다.
뭐 특이점이거나 높은 지렛점이라고 해서 무조건 영향력 관측치인 것은 아니기에, 고려해야 할 점을 알아보겠다.
1. 어떤 추정량에 영향을 끼치는가?
beta_hat에 영향을 많이 끼치는 관측치더라도 표본분산에 무조건 큰 영향을 끼치지는 않는다.
따라서 이를 파악해봐야 한다.
2. 각각의 영향력인지 vs 관측치군의 영향력인지
i, j번째 관측치가 각각 beta_hat에 대한 영향력 관측치여도, i와 j를 동시에 고려한 영향력은 작을 수도 있다.
반대의 경우도 있다. 그래서 각각의 영향력이 큰 것은 '개인적 영향력 관측치' 혹은 '영향력 관측치' 라고 부르고,
둘 이상의 관측치들을 묶어서 조사할 때 영향력이 크다고 판단되는 것은 '영향력 관측치군'이다.
영향력 측도
영향력을 판단하기 위한 기준이라고 생각하면 된다.
보통 소거법을 사용하는데, 모든 관측치로 계산한 추정값 vs i번째 관측치를 제거한 추정값 이렇게 비교하는 방법이다.
일반적으로 사용하는 측도로는 쿡의 거리 통계량, DFBETAS, DFFITS이 있다.
