본 게시글은 충남대 정상근 교수님의 강의자료를 바탕으로 작성한 글입니다.
Gradient Clipping
보통 경사하강법을 진행할 때 Loss function의 미분값과 Learning rate를 곱한 값을 이용해 파라미터 업데이트를 진행한다.
근데 만약 미분값이 너~무 크다면, 예를 들어 거의 수직으로 떨어지는 곳이라면.. 내가 원하는 지점이 아닌 다른 지점으로 업데이트되게 될 것이다.
그래서 만약 기울기의 L2-norm인 ||g||가 일정 임계값(Eta)을 초과하면 이를 Eta*g/||g|| 로 rescale한다. 그 방향만 가져가는 것이다.
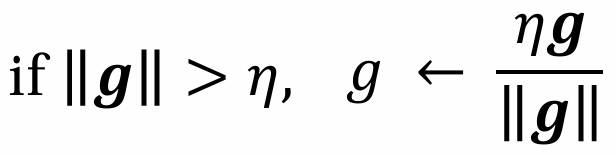
이렇게 하면 실제 gradient가 아니기에 bias가 유도될 수도 있긴 하지만, 학습 안정성이 증가하게 된다.
이게 gradient clipping이다. 임계값을 초과하면 자르기!
참고로, pytorch에서는 clip_grad_norm_으로 사용할 수 있고, keras에서는 optimizers.SGD의 clipnorm 또는 clipvalue를 통해 사용할 수 있다.
Learning Rate Change
위에서는 경사하강법의 '미분값'을 조절하는 내용에 대해 알아보았다.
이번에는 그 미분값에 곱해지는 learning rate를 어떻게 조절할지 알아보겠다.
학습률은 손실 함수의 형태에 따라 최적값이 달라진다.
Step Decay 방식이라면 일정 시점마다 학습률을 계단처럼 감소시킬 것이고,
Warmup 방식이라면 작은 학습률에서 시작해 점진적으로 증가할 것이고,
Cyclic LR 방식이라면 학습률을 주기적으로 증가 혹은 감소시킬 것이다.
Cosine Annealing
이건 그냥.. new 학습률을 구하는 과정에서 cos을 사용한 것임!
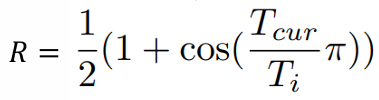
이 학습률 변화를 Transformer에 적용하면, Warmup을 적용할 수 있고,
GPT3에서는 warmup + cosine decay를 적용한다.
L2 Regularization
L2 정규화는 '작은 모델을 원한다'는 관점에서 시작됐다.
큰 weight는 과적합을 유발하기 때문에, 작은 weight를 선호하게 된다.
따라서 손실함수에 L2 penalty 항을 추가하는 것이고, 이걸 L2 정규화라고 한다.
예를 들어, 가중치가 W = [32, 52, 3, 65, ..., 1.5] 이런 식으로 된다면,
이 가중치를 각각 제곱한 것의 합, 즉 L2-norm을 구한다면 이걸 손실함수로 사용하여 모델의 크기를 줄일 수 있을 것이다.
보통 정규화 손실함수는 아래와 같이 작성하고, lambda가 0이라면 정규화를 진행하지 않는 것이 된다.

Weight Decay
이또한 큰 가중치 억제로 일반화 성능 향상을 위한 것이다.
하지만 위 L2 정규화는 손실함수 자체를 바꾸는 것이고, Weight Decay는 optimizer가 파라미터를 decay시킨다는 점에서 차이가 있다.
L2 정규화는 목적함수가 아예 바뀌어서 최소한의 손실을 내도록 하는 것이고,
Weight Decay는 매번 파라미터 업데이트 시 파라미터가 자동으로 감쇠(decay)되며 최적화되는 것이다.
그래서 L2정규화는 정규화 항이 gradient에 직접 더해지는 것이고, decay는 gradient 와 독립적으로 적용되는 것이다.
아래 그림과 같이 기존 파라미터에 가중치를 두는 형식으로 사용된다.

근데 이 weight decay가 갑자기 왜 나왔냐면,
SGD에서 L2 정규화와 Weight Decay가 수학적으로 유사하기 때문이다.
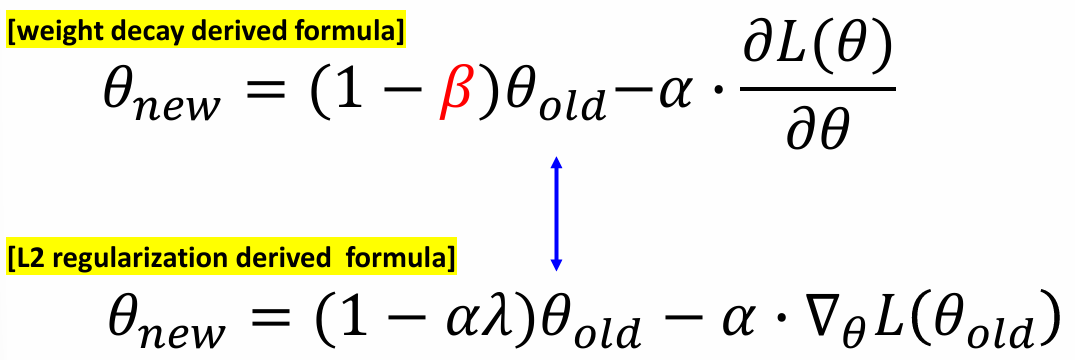
이 형식이 되므로, 만약 beta = alpha * lambda 라면 두 식은 정확히 같게 된다.
그리고 보통 pytorch나 tensorflow에서 weight_decay를 0.01로 지정하게 된다면,
beta값이 아닌, alpha와 곱해지는 lambda값이 0.01로 지정되는 것이다.
'AI > 자연어처리' 카테고리의 다른 글
| T5 model (3) | 2025.06.13 |
|---|---|
| AMP, Quantization (1) | 2025.06.13 |
| LoRA(Low-Rank Adaption) (3) | 2025.06.12 |
| PEFT(Parameter Efficient Fine-Tuning) (1) | 2025.06.11 |
| 언어모델 (0) | 2025.04.29 |
